最近在学习 NLP 领域中的主题模型 Topic Model 模块,从简单的二元混合文档 Mixture Model 开始,到复杂一点的多主题模型 PLSA,一直到最复杂的 LDA 算法,不论是听课,还是看别人的博客,看完后,我都是处于一种一知半解的状态,云里雾里,也去翻了很多的资料,也没能看明白是怎么一回事儿。
直到最近我终于下定决心,拿起纸和笔,自己一点一点的推导公式,一步一个脚印的拿着 EM 算法,来演算一遍这个求解过程。等推算一遍下来,我终于算是搞明白了算法是怎么一回事,以及它是怎么被计算出来的了。这篇博客就是主要用来记录我的推演过程,同时也希望这篇文章是一篇非常通俗易懂的博文,能帮助大家快速清楚明白的看懂这个模型,不必像我一样,再去走很多的弯路了。
这篇文章我先介绍 PLSA,之后我会再写一篇文章来介绍 LDA 算法。
Topic Model
先来介绍一下主题模型究竟是个什么东东。其实说白了,就是一个用来分析文章的主题的玩意儿。
举个例子,新浪的小编今天收到一份投稿,在审核完了这篇文章符合十九大精神,且并没有什么导向性错误之后,小编决定将它发布到新浪新闻的网站上去了,发布之前小编需要选择,这篇新闻我究竟是应该发在军事栏呢,还是应该发在体育栏呢?OK,这个时候,我们就发现,哦,原来一个文章是有主题的。并且我们可以通过主题来归类文档。
恩,但是一个文章可能会有多个主题,比如小明写了一篇文章,《从 NBA 球场看中国经济的发展》,这篇文章可能前半部分谈论的是说体育,后半部分说的是经济。那这个时候,我们怎么来定量的来表示文章的主题呢,我们会说文章里面百分之四十是体育主题,后面百分六十是经济主题。
OK,现在,我们的主题模型就初具雏形了。不过,在 NLP 里面,我们除了特定的主题外,我们一般会加上一个特殊的分类,叫做无主题类 Background。每个主题各自占比多少,就是由单词的数量来决定的。是不是很简单粗暴呀。

举个直观的例子,上图是一篇关于飓风 Katrina 的博文。红色部分的主题是政府的举措,紫色部分的主题是现场时事的报道,绿色部分说的是捐款和赈灾的情况。而黑色的部分是无任何主题的,我们称之为 Background words。通过不同颜色文字占的比例,我们可以一眼看出文章主题的分布是如何的。
PLSA
PLSA 算法,就是基于一个文章可能具有多种主题的这种情况,进行的建模。通过该算法,我们的最终目标是要得到两个东西。
- 对于文档库中的任意一个文章,我想要知道这个文章各个主题的占比是多少。
- 一个文章中的特定单词,它是属于某个主题的概率是多少。
第一个目标好理解,即是说,通过计算,我们要知道文章《从 NBA 球场看中国经济的发展》中,体育占比 0.35,经济占比 0.5,无主题的 Background Words 占比 0.15。
那么第二个目标什么意思呢?举个例子,假如在一大段文字中,你看到了单词“比赛”,现在你要猜测 “比赛” 这个单词是出现在关于主题 “体育” 中的一段话中呢?还是出现在属于关于 “娱乐” 的一段话中呢?
生活经验告诉你,“比赛” 这个单词出现在 “体育” 主题的文字中的概率,比出现在 “娱乐” 主题文字的概率,要大一些。那如果我们用数字来描述它的话,可能它出现在体育的概率是 0.7,出现在娱乐中的概率是 0.2,出现在无主题文字中的概率是 0.1。
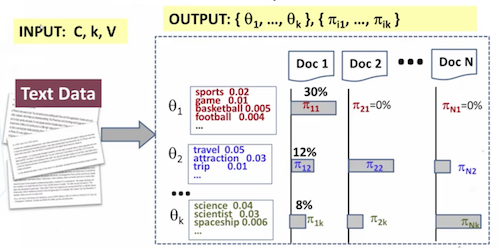
用一张图来解释一下 PLSA 算法的目标。左边部分是我们的输入:一大堆文档。右边部分是输出,每个文档对应的主题占比,以及每个单词对应的属于某个主题的概率。
Generate Text with PLSA
在正式的求解之前,我们来开一个脑洞,反向的来思考一个问题。现在我们不再是已知文章求主题,而是已知一个文章是由音乐,体育,政治和无主题组成,并且知道每个主题的占比,以及在每个单词在该主题中出现的概率是多少,通过这些值,我们的目标是生成一个文章。
这看上去有点不可理喻,仅仅凭一些主题的占比,以及单词出现的概率分布,就想生成文章?好像觉得是不可理喻的。但是,现实生活中,我们确确实实是有这样的例子的。我们可以想象一个作家在写文章之前,他其实心里是预设好了我要写哪些主题的东西的。然后每个主题涉及到的词,一般来说,如果不是刻意去回避的话,都会按照概率的大小去使用到。这样想想,这种脑洞好像也并不是完全无稽之谈。
既然这样,我们就大概估计着定义一些单词和出现在主题里的概率分布。
- 无主题的文字占比为 0.2。
- 有主题的文字一共由三个主题组成:音乐 50% ,体育 30% ,政治 20%。
- 下面是我们词库里的单词,三个单词属于各个主题的概率见下表。

有了这些信息之后,我们开看看这个“作家”会如何根据主题和概率的分布来写文章吧。千里之行,始于足下。要想生成一个文章,我们要一个一个单词的来。首先,他要写第一个单词。
我们来推测一下,我们的这位作家,他会写哪一个单词呢?这就需要我们得到每个单词被他写的概率。
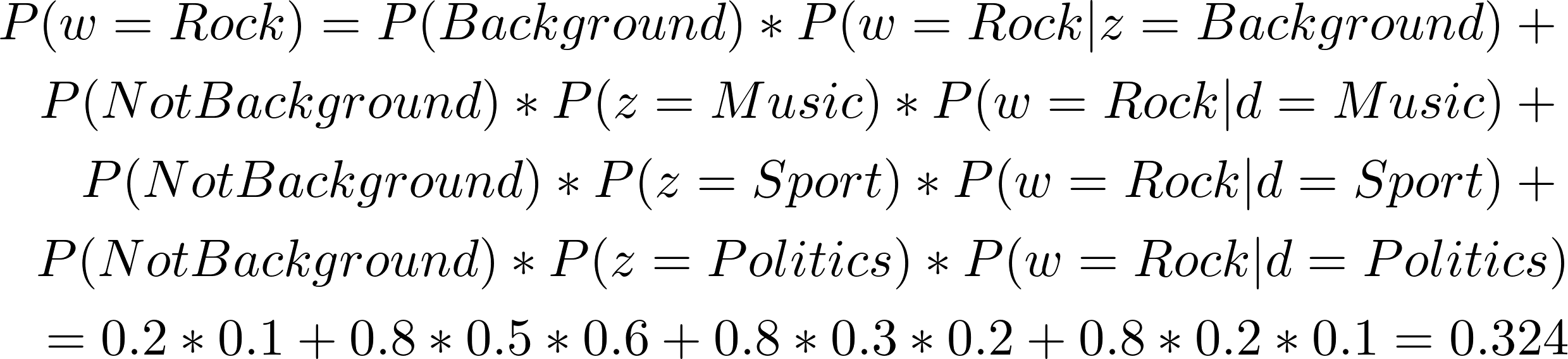
上面的公式是由贝叶斯公式计算得来的,我们知道当前的概率分布后,得到作家写第一个词是 Rock 的概率是 0.324,同理,我们可以得到第一个词是 Basketball 的概率为:0.266,第一个词是 Policy 的概率为:0.194。
如果我们把上面的过程用一张图来表示的话。就是如下的过程。

这张图我们需要从右下角出发。作家首先要做的是进行一个选择,是选择写无主题的背景单词呢,还是有主题的单词呢。如果是有主题的单词,写主题 i 的概率是多少呢?然后如果是写主题 i,主题 i中出现单词 w 的概率又是多少呢。这是其中的一种情况,我们需要用乘法法则来求解,如果是全部的情况的话,就是需要用加上把所有的概率加起来了。
写完第一个单词之后,就可以看写一篇文章了。其实每次作家做的事情都是重复写一个一个单词的过程。
EM Parameters
通过之前的讲解,我们知道了主题模型 PLSA 算法的目标以及它的输入输出,那么我们要求解的参数,怎么计算得到呢?
这个时候,我们就要引进 EM 算法,来帮助我们求解了。EM 算法具体原理和推导并不是这一片文章要介绍的,我们只是看一下在 PLSA 中利用 EM 来求解。
要利用EM来求解。首先,需要确定哪些参数是未知的。下图的公式中,显示了未知的参数分为了两个部分,
- Πd,j指的是在文档 d 中,主题 j 占的比例。
- θj指的是在主题 j 中,各个单词出现的比例。

这也很好理解为什么需要这两组参数,因为实际上,如果有了每一个文档的主题的占比和每个主题单词出现的频率,一个生成模型就呼之欲出了。
EM Process
明确了参数,那么来看一下EM的求解过程吧。EM 算法的精髓在我看来其实是两个。
- 1. 引入一个合适的 hidden vector 隐藏变量。
- 2. 找到一个可自收敛的 E 过程 和 M 过程来将需要求解的参数。
首先来看第一个问题,PLSA 的EM 过程中隐藏参数的定义

上图中的 Zd, w 就是隐藏变量,它代表的是在文档 d 中单词 w 属于某一个主体的这一个事件,我们的 E 过程就是计算这个 Z 事件的概率。

M 过程通过隐藏变量来重新估计 E 过程中的两个输入。至此,EM 终于得到了收敛。
Write At The End
这一篇 blog 历时四个月,之前在12月的时候写了一半,现在才将它补齐。很多东西在第二次写的时候已经忘记了,这再次说明了趁热打铁,当时明白就要马上写下来的道理。以后再接再厉。