这篇博客主要介绍网络的生成和演变过程,和对应的几种来模拟这种生成的过程的模型,最后介绍预测可能的链接的方法。
Degree Distribution in Real-World Network
节点的 Degree 描述的是当前节点与其他节点的连接的个数,例如一个人和多少个人是朋友, 通常我们会比较关注的是无向图中的 Degree 和有向图的 In Degree,因为他们通常会描述的是节点的 Popularity。
那么真实世界中的节点的 Degree Distribution 长什么样子呢? 我们通过下面三个例子来看一下吧,其中:
- 图 A 中的节点 Degree 分布描述的是 225 000 个演员共同出演电影的情况。
- 图 B 描述的是 325 000 个网络界面 link 的指向情况。
- 图 C 是 4 941 个电力网络节点的连接图。
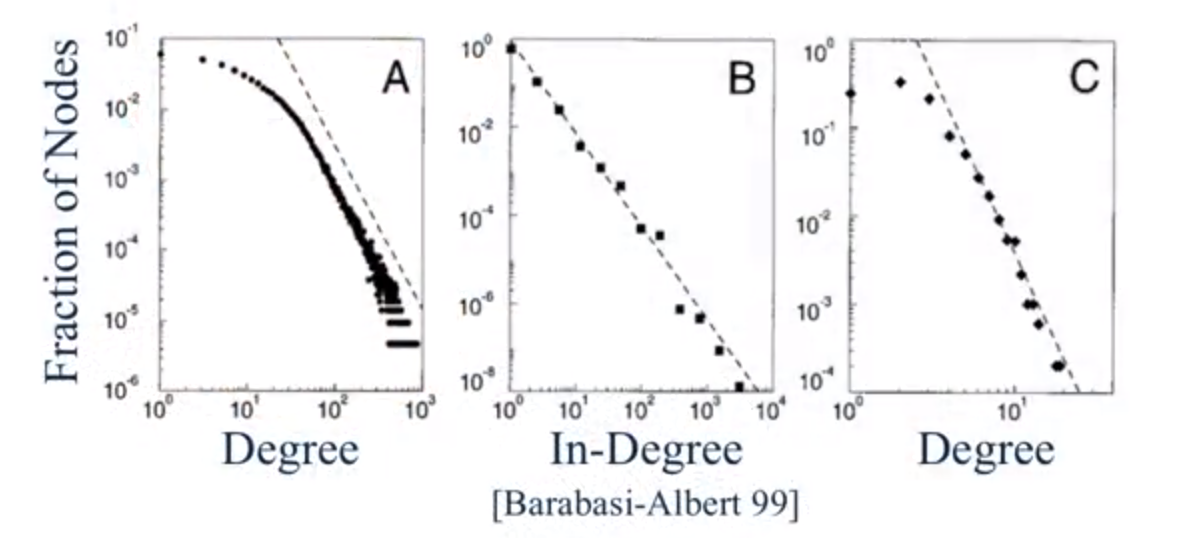
上图中画出的是节点 degree 到这个 degree 的节点在图中出现概率的映射, 需要注意的是,这些坐标轴都是 log 的对数处理过的。
通过形状, 不难看出,经过对数处理的分布图基本呈线性分布, 图中的虚线代表了线性走向的趋势,是一种类似于递减的一次函数分布. 但由于坐标轴做了对数处理,所以出当节点连接数增加的时候,出现的概率呈指数下降趋势。
用数学模型来表示这种趋势的话,就是一种 power law 的分布情况

其中 C 和 α 是常数,k 是节点的 Degree ,P ( k ) 是这种 Degree 出现的概率。
实际上, 大多数的真实世界的网络都遵循着 power law 的分布, 而 α 的值一般在 2 到 3 之间。
Preferential Attachement Model
我们知道真实世界的网络遵循着 power law 的分布, 那么有没有一种模型可以模拟这种生成过程的呢? 答案是肯定的.
Preferential Attachement Model(以下简称 PAM) 是随机生成以上具有这种特征的网络的模型,它的基本思路是如果一个节点的连接的节点越多,那么它接收新连接的可能性就越大。 具有更高 Degree 的节点具有更强的抓取添加到网络中的链接的能力。
是基于以上的假设,PAM 的算法过程如下:
- 从两个已经连接上的节点开始生成网络。
- 在每个时间步骤中,添加一个新节点,并将其连接到现有节点。
- 随机选择要连接的节点,其概率与每个节点的 Degree 成正比。
- 连接到节点 u 的概率是 Degree ( u ) / Sum_of_All_Degree。
下图就是一步一步从两个连接的节点开始,生成图的过程,红圈中的节点是当前步骤需要插入的节点,其他的节点是已经存在于网络中的节点,其中每个节点上方的数字代表的是在插入节点时,根据它的 degree 计算出来的概率。
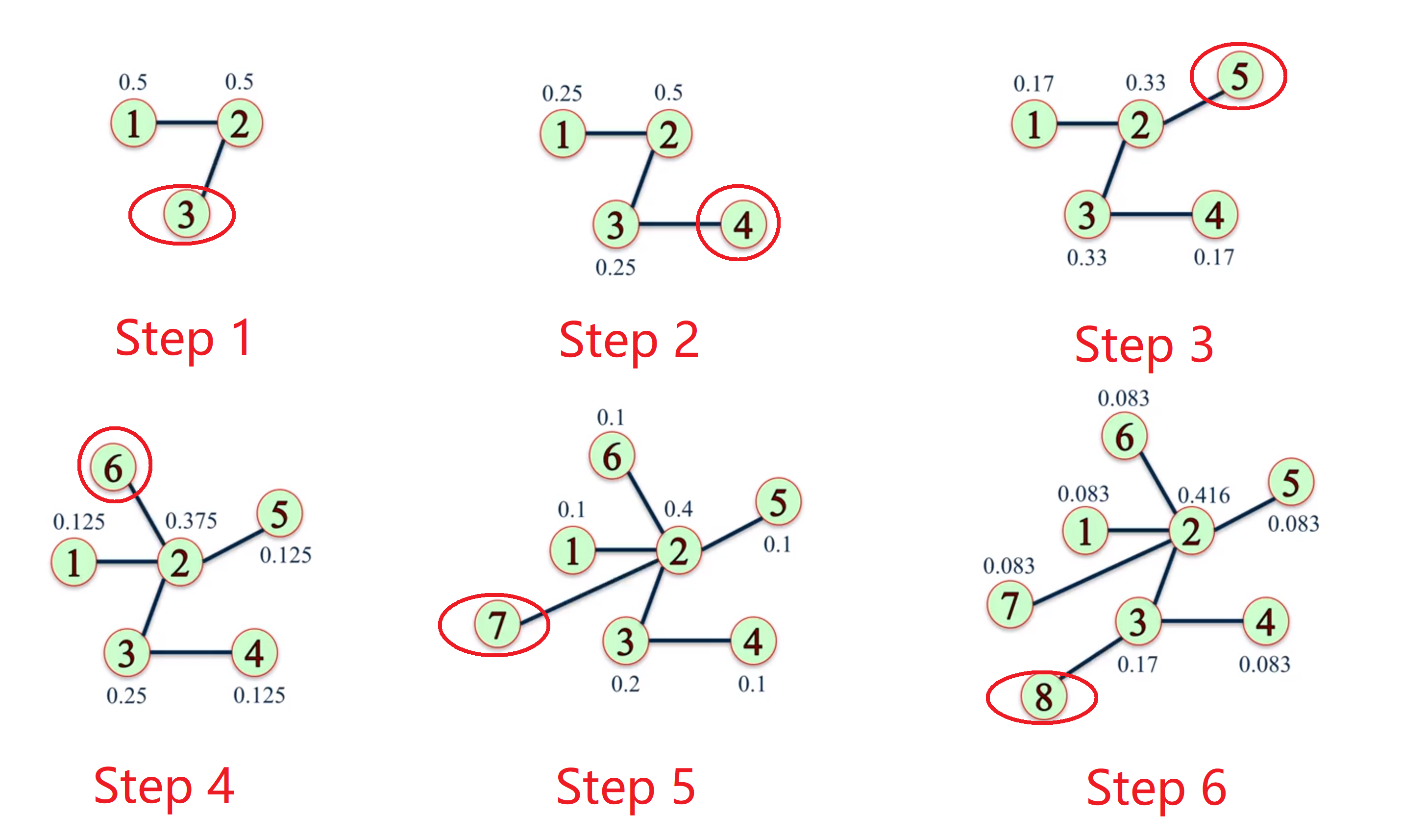
我们无法通过严格的数学证明这种生成图方法的正确性, 但如果抛开严格的证明, 只是从那感觉上来说, 这种生成方法是可以说的通的.
在社交网络中, 有很多连接的节点代表着众多关系密切的知名人士。 当一个新人进入社区时,他/她会更倾向于认识一个更明显的人,而不是相对未知的人。
假设在万维网中,新的网页优先链接到有很多连接的网站,即非常知名的诸如Google之类的网站,而不是任何人都不知道的网页,所以如果有人通过随机选择现有链接来选择要链接的新页面,则选择特定页面的概率将与其 Degree 成正比例。
我们来看一个由 PAM 生成的包含 1 000 000 个节点的图的 degree 概率分布吧。
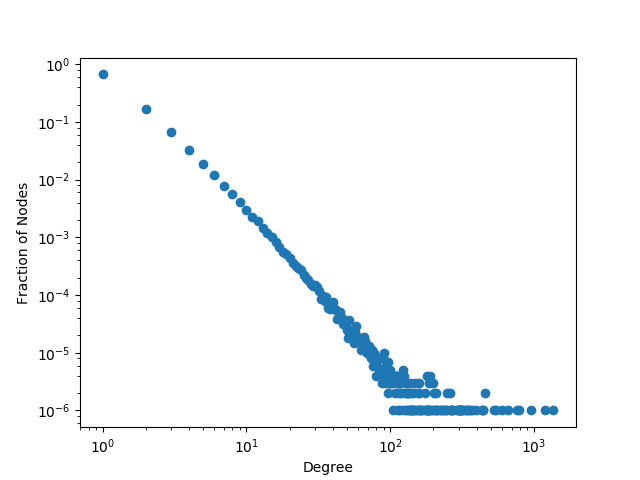
它确实和我们之前看到的真实世界中的分布是很类似的。
这种生成图模型的方法也被叫做 Barabasi Albert Graph,是为了纪念发明它的人而命名的。
Rich-Get-Richer Model
Rich-Get-Richer Model (以下简称 RGR)和 PAM 的出发点类似,都是认为 Degree 更高的点具有更强的吸附新节点的能力。(看这个模型的名字。。。)
RGR 模型算法的大多数不走和 PAM 是一样的,只有稍稍有一点改动,就是在新节点插入的时候,会有一定的概率 p 不去 attach 到已经存在的节点,而是 attach 到那个节点连接的节点。
这样做的原因是,PAM 模型中最后求得的指数的系数 α 的值,通常都是 2,但是 RGR 模型由于有这个 p 的存在,指数系数就不一定是 2 了,它的大小则是由 p 的大小来决定的,这个更贴近真实生活中的情况。
Milgram Small World Experiment
很多人可能听说过,世界上的人,只要经过短短 6 次连接,就可以相互认识。那么这个结论是怎么来的呢?实际上它的来源, 是一个非常有名的实验, 叫做 Milgram Small World Experiment。
这个实验的做法是,在美国波士顿市随机的选择 249 个人,让这 249 个人分别去送信,信的接收方是随机选取的,但接收方的基本信息会被提供给送信的人,比如接收房的姓名,性别,年龄,职业等。
送信的人如果认识接收信的人的话,就送给他,如果不知道的话,就将信交给一个他认识的并且觉得可能会认识这个人的人。
这是一个非常有意思的实验, 在它结束的时候:有 64 / 296 的信件被成功送达了,送达平均需要传递信件的次数大约是6,分布从 0 到 11 不等。
通过这个实验, 我们可以得到以下两个很有意思的结论:
- 1. 人们是有着自主发现最短路径的能力的。
- 2. 很多情况下,真实世界的人是可以相互通过很短的连接互相认识的 (平均 6 次即可)。

当时的人们做这个实验的时候,并没有大数据,也没有计算能力可以计算得到真实的连接数。
现如今,我们有着像 Facebook, Microsoft Instant Messager 等等让人们相互连接的网络,通过计算,在 Facebook 上,人与人之间的距离是 4.74 (2011年),Microsoft Instant Messager 的距离是 7 (2008年)。所以实际上当年人为做实验的数据得到的 6,三十年前的实验结论基本也是对的。
Friend of a Friend
真实的社交网络中,一个人的朋友的朋友可能和他也是朋友。这种指标在图中可以用 Local Clustering Coefficient (以下用 LCC 来表示)来表示。一个随机生成的图,它的 LCC 值会非常的低,但是在真实的网络中,这个 LCC 值往往很高。下图是 Facebook 在 2011 年的 LCC 的值
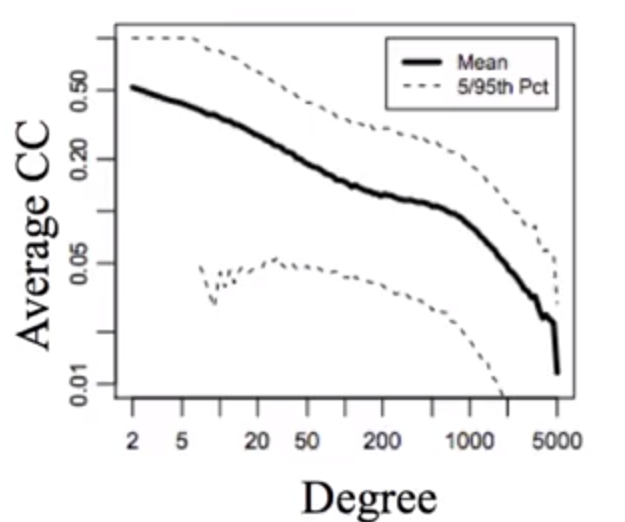
Small World Model
不难看出,真实世界的社交网络有着明显的两个特征:
- 人与人之间的距离很短: Avg Distance 小
- 连接呈现出 Cummunity 的趋势: LCC 较大
前面的 PAM 和 RGR 模型,他们生成的网络只能曼度第一个条件,而第二个条件则无法满足。原因是,新加入的节点更倾向于和 degree 高的节点进行连接,所以节点距离往往不会太远,但是新节点之间的连接却不能保证,所以 LCC 值不会很高。
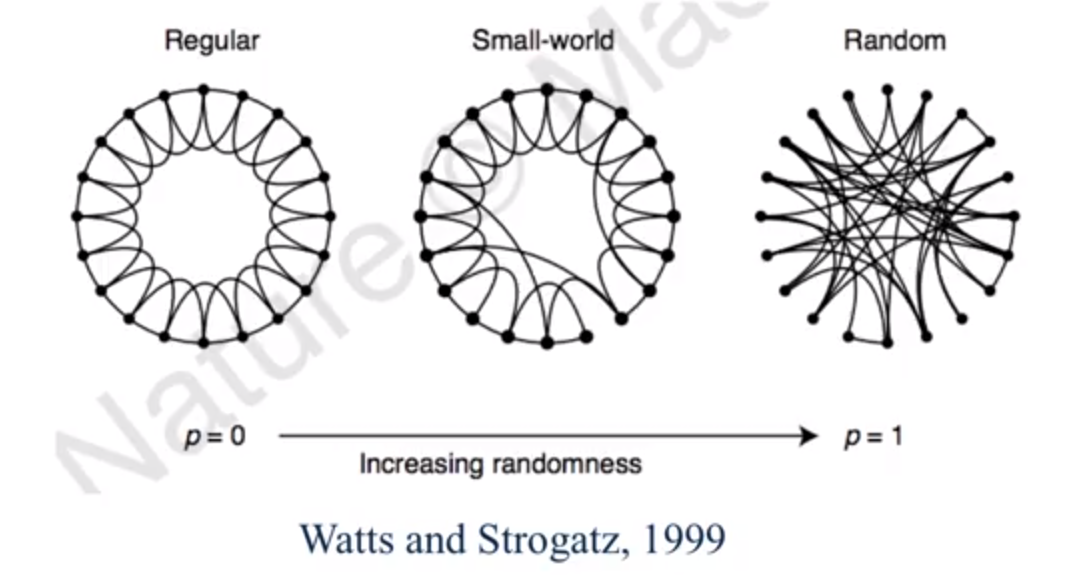
现在介绍的一种图的演变生成模型,Small World Model 则是可以生成一个同时满足这两个条件的网络的。他的生成过程如下。
- 1. 将图的节点生成成一个环的形状。
- 2. 定义一个概率 p
- 3. 遍历每一个节点 u - v,根据概率判断是否会重新连接节点,如果需要的话,就断开 u - v 的连接,将 u 随机的连上节点 w。
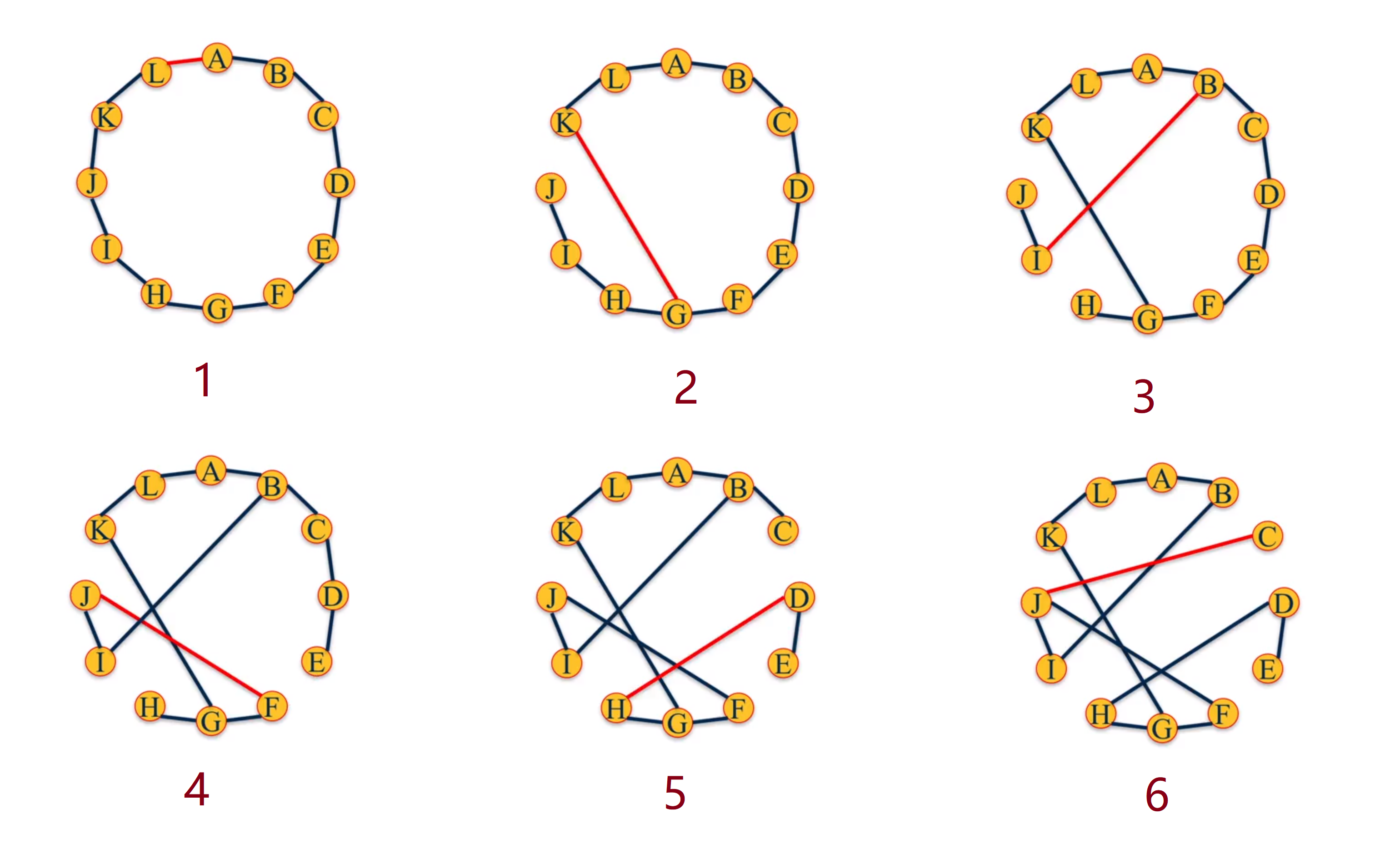
其中没有变动的链接表示按照当前的概率计算,它不需要重新连接,图中只显示了根据概率而重新连接的边。
所以在生成一个 Small World Model 的图的时候,有三个参数是需要给定的:
- 1. 图有多少个节点
- 2. 平均每个节点会与多少个其他节点连接。
- 3. 有多大概率重新连接边
概率的大小直接影响了最终生成图的 LCC 和 Avg Distance。p 越大,距离越小,LCC 越高,但是图原本的结构就会遭到破坏,所以一般情况下,我们会选择 0 到 0.1 之间的概率来生成这个图。
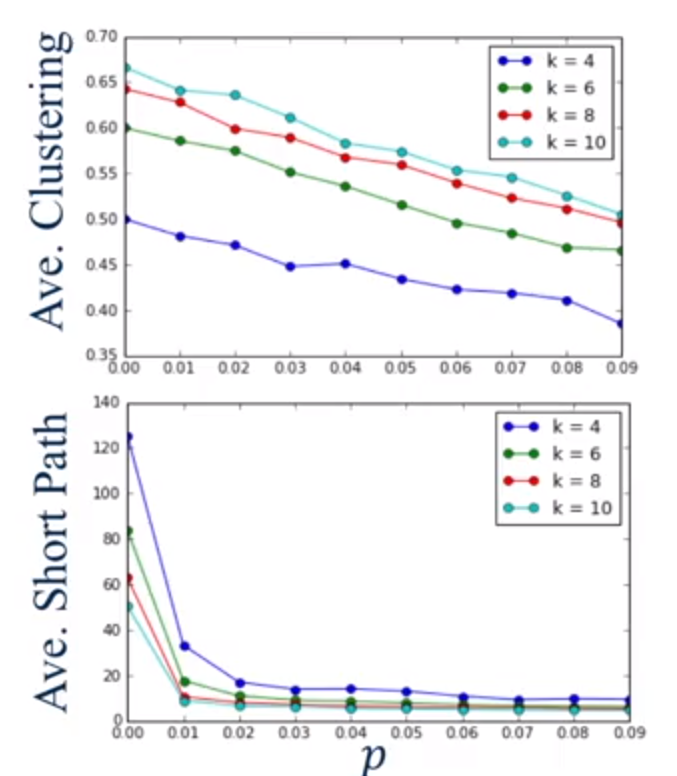
上图中显示了,通过 Small World Model 生成出来的模型,满足了 Low Distance 和 High LCC 的要求。
这种生成图的方法也被叫做 Watts Strogatz Model,也是为了纪念发明它的人。
有的时候,Small World Model 生成的图会是断开连接的图,为了避免这种情况(因为大多数的时候,我们是希望生成一个连接图)。解决方法一般有两个:
- 可以在重新连边的时候,进行判断,如果此时是断开了的话,就再重新尝试连接,这种方法叫做 Connected Watts Strogatz Model
- 或者不重新连接,而是加上一条连接,这种方法叫做 Newman Watts Strogatz Graph
Predict Link
给定一个网络,如何判断哪些节点可能会被连接上。这也是在图的演变过程中很重要的一项研究,这里给出五种判断指标和两种特殊对于 community 中的连接预测的指标。
1. Common Neighbors
用两个节点间的共同邻居的数量来判断是否有趋势连接到一起。
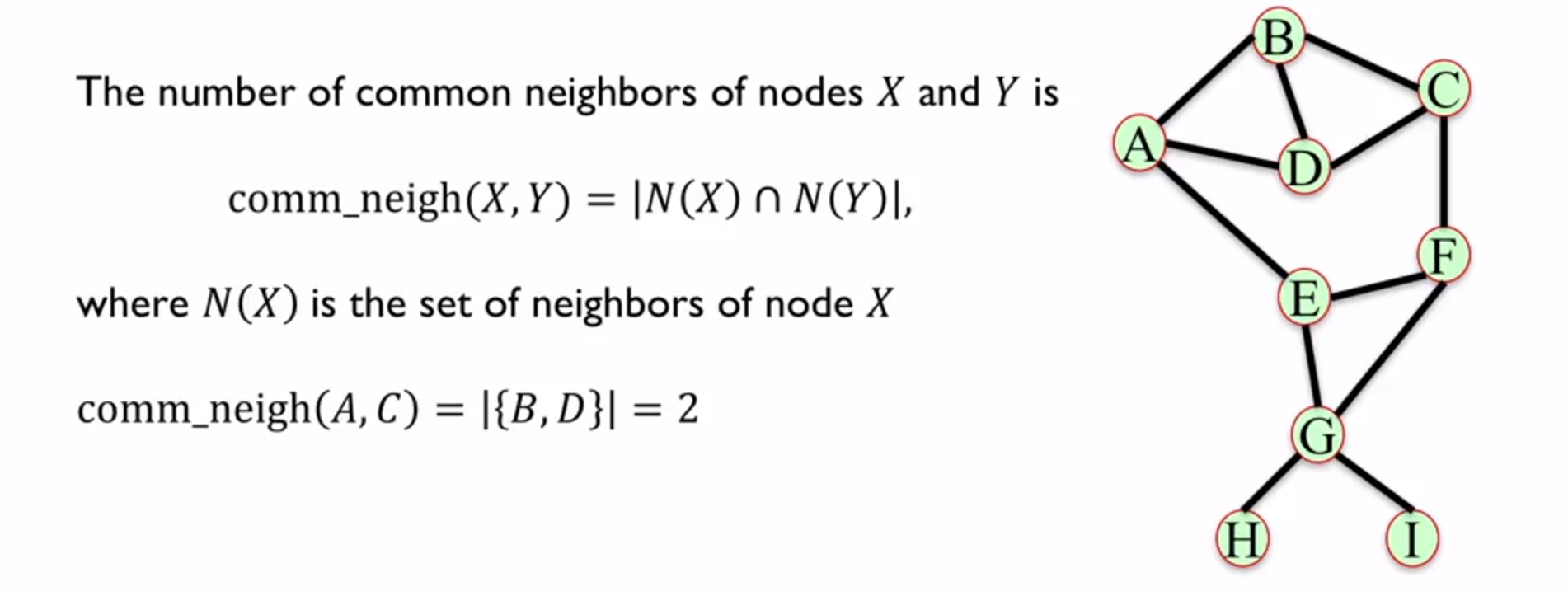
2. Jaccard Coefficient
用共同邻居的个数 除以 所有邻居的个数
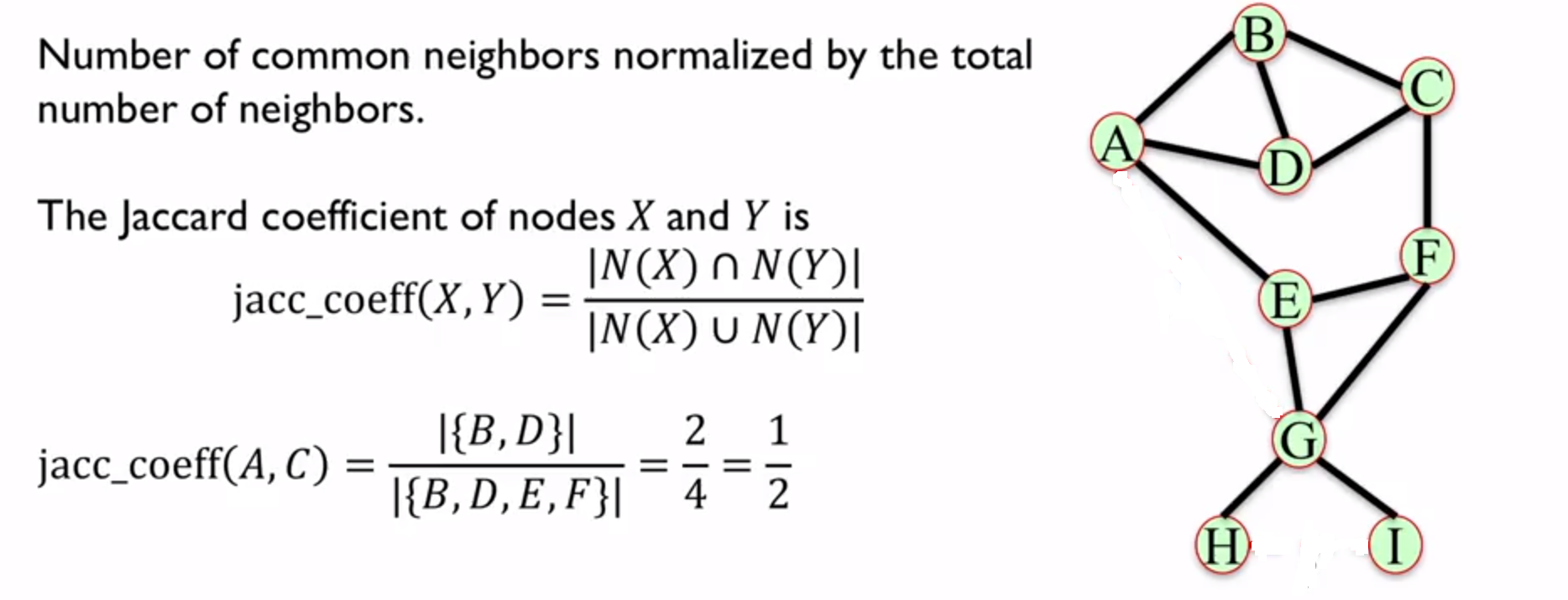
3. Resource Allocation Index
共同邻居的 Degree 的倒数的和
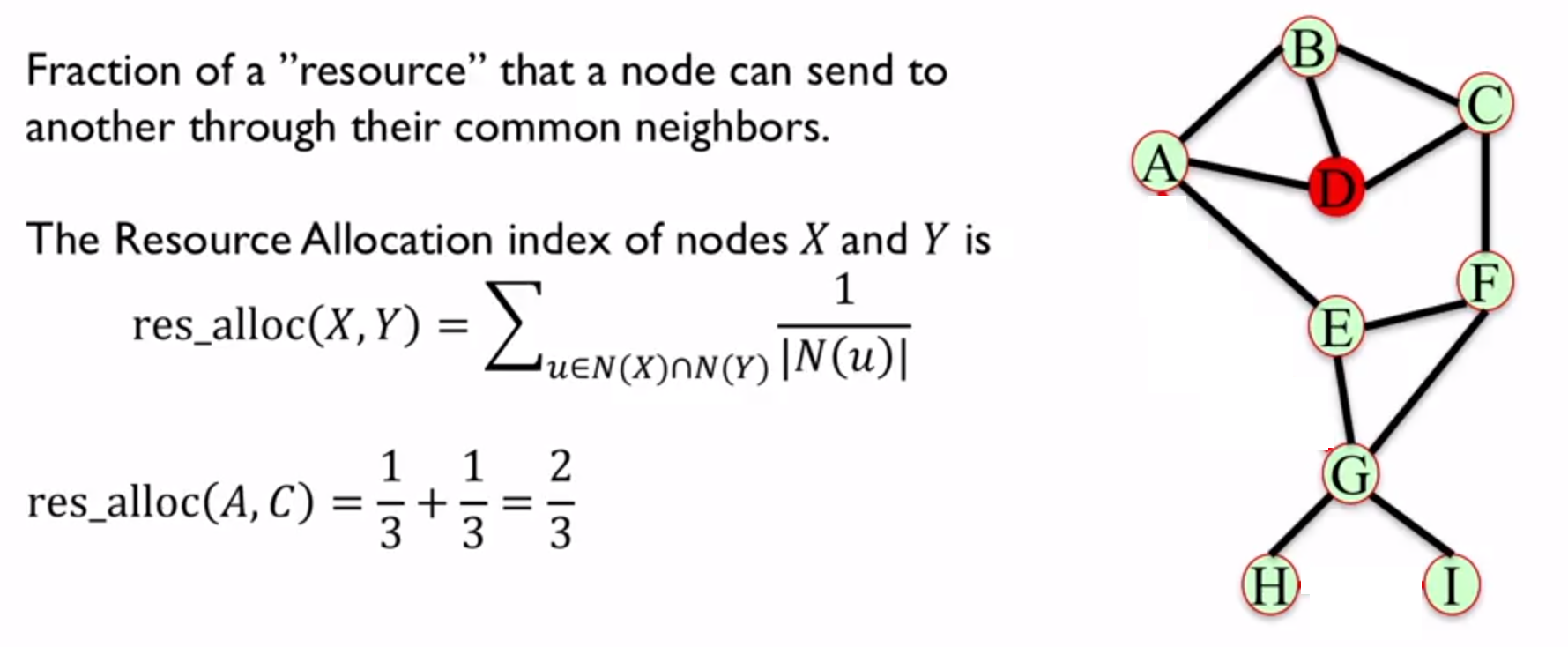
4. Adamic-Adar Index
共同邻居的 Degree 的对数的的倒数的的和
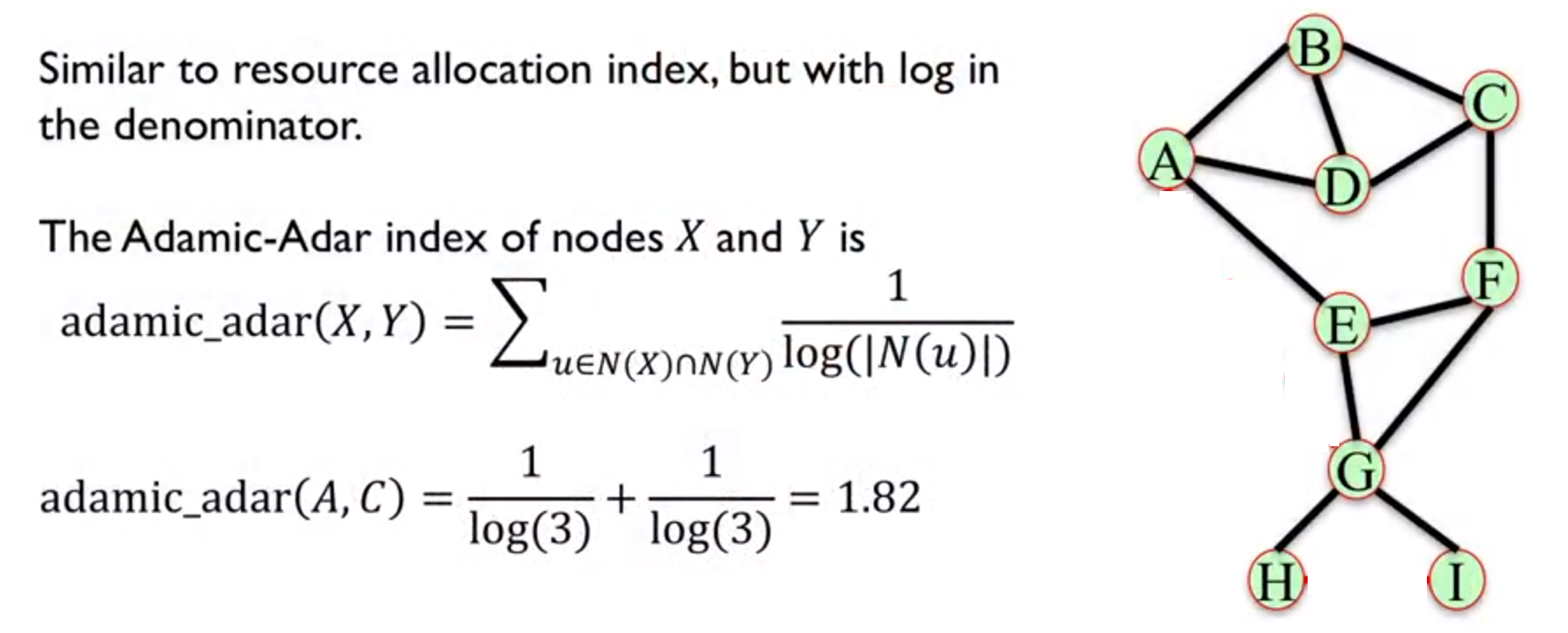
5. Preferential Attachment
受 Preferential Attachmen Model 的启发,Degree 高的节点更容易连接到别的点,用两个节点的 degree 的乘积来表示连接倾向。

6. Community Common Neighbors
和 Common Neighbors 类似,只不过给与在同一个 community 的共同节点更多一点权重。

7. Community Resource Allocation Index
和 Resource Allocation Index 类似,不过只计算在同一个 community 的共同节点。

Conclusion
这篇文章主要是为了记录了我在学习图的生成演变过程的学习笔记,我也是最近才开始了图分析的研究和学习,以前完全不知道有这样的一些东西,慢慢的经过学习,了解更多后,感觉像是打开了一个新世界的大门一样,图分析的研究还是很有意思的。