[Graph] 图分析--聚类系数，节点距离，联通子图和图的稳定性分析


介绍四个基本的图分析

Posted by Yufan Zheng on May 4, 2018

最近公司开始要做 Social Media 方面的项目了，为了能更好的做这个项目，我也开始了Social Network Analysis 的研究和学习，这一篇博客记录下我在学习社交网络分析时接触到的几个概念。

Cluster Coefficient

在谈到 Cluster Coefficient（聚类系数）之前，先介绍一个概念，叫做 Triadic Closure。Triadic Closure 指的是在一个三角形中，有两个边已经连接上了，只有一个边是断开的和一种情况。

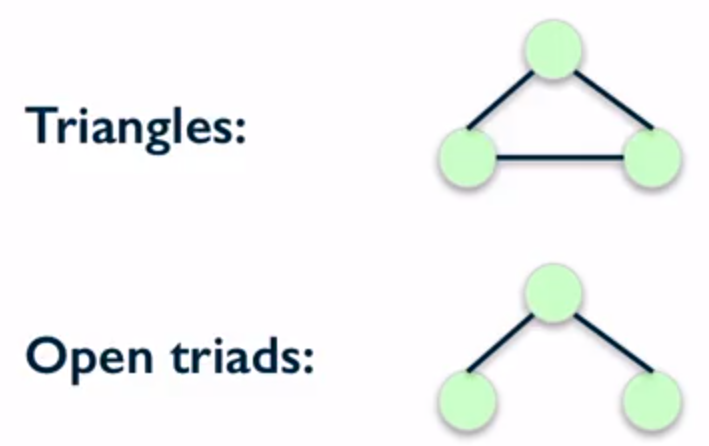
不难看出，在一个图模型中，如果出现了上图所示的这种连接的话，未连接的两个节点会有趋势被连接上。那些在网络中快要形成三角形但是还没有形成的，就是我们需要的。在一个连接图中找 Triadic Closure，会非常的有用。比如可用于发现社交网络中，还未连接的，但可能成为好友的人。

基于 Tradic Closure，我们可以定义图的聚类参数。我们先从如何计算一个节点的聚类参数开始说起。

Local Cluster Coefficient

一个节点的聚类参数被称为 Local Cluster Coefficient。它的计算方法也是非常的简单粗暴。先计算所有与当前节点连接的节点中间可能构成的 link 有多少个，这个数会作为分母，然后计算实际上有多少个节点被连接上了，这个数会作为分子。最终的计算结果就是 Local Cluster Coefficient。

举个栗子，上图中的节点 C 的 Local Cluster Coefficient 就是 1⁄3。

Global Cluster Coefficient

知道了如何计算单个节点的聚类系数，现在来看如何计算整个图的 Cluster Coefficient。

一种最简单粗暴的方法是，先计算每一个节点的 Local Cluster Coefficient，然后取平均值。

第二种方法，是先计算在图中已经关闭上的三角形的个数，除上没有闭上的三角形的个数。这种计算方法叫做 Transitivity。

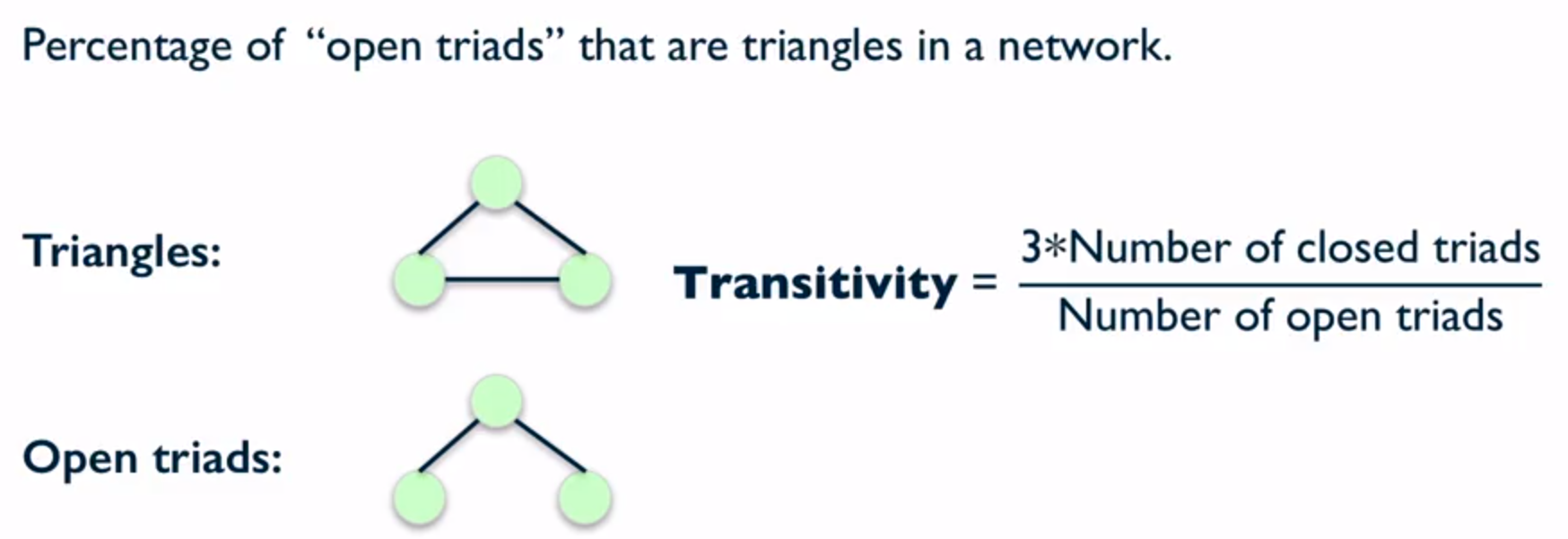
这两种方法并没有优劣之分，只是 Transitivity 会倾向于给 degree 大的节点较大的权重。

Node Distance

节点距离，指的是两个节点间的最短路径的长度。为了获得最短距离，通常可以采用图的深度优先遍历，或者广度优先遍历。对于一个较大的网络，想要获得从一个节点到所有节点的距离，会推荐使用 广度优先遍历，因为广度优先遍历可以一层一层的进行计算距离。

接下来介绍几个用于描述网络节点距离的参数

  • Average distance： 这个很好理解，就是所有两两节点之间的最短距离的平均值，最直接的描述了图的紧密程度。
  • Eccentricity：这个参数描述的是从任意一个节点，到达其他节点的最大距离
  • Diameter：图中的最大两个节点间的距离
  • Radius：图中的最小两个节点间的距离
  • Periphery： 和 Diameter 对应，那些最大节点距离等于 diameter 的节点
  • Center： 和 Radius 对应，那些最大节点距离等于 radius 的节点

利用 Python 来计算这些参数的示例代码如下：

# Example code using networkx
import networkx as nx

G = nx.Graph()
G.add_edges_from([('A', 'K'), ('A', 'B'), ('A', 'C'), ('B', 'C'),
                  ('B', 'K'), ('C', 'E'), ('C', 'F'), ('D', 'E'),
                  ('E', 'F'), ('E', 'H'), ('F', 'I'), ('I', 'J')])

# ==> Average distance (Average Shortest Path Length)
print(nx.average_shortest_path_length(G))
# 2.3777777777777778

# ==> Diameter
print(nx.diameter(G))
# 5

# ==> Eccentricity
print(nx.eccentricity(G))
# {'K': 5, 'I': 4, 'E': 3, 'D': 4, 'H': 4, 
#  'B': 4, 'A': 4, 'F': 3, 'C': 3, 'J': 5}

# ==> Radius
print(nx.radius(G))
# 3

# ==> Periphery
print(nx.periphery(G))
# ['K', 'J']

# ==> Center
print(nx.center(G))
# ['E', 'F', 'C']

Connected Components

满足子联通图的充分必要条件有两个：

  • 1. 子连通图中的每个节点都可以有路径可以连接到其他节点
  • 2. 任何其他非连通图单位的节点都没有路径可以连接到该连通图

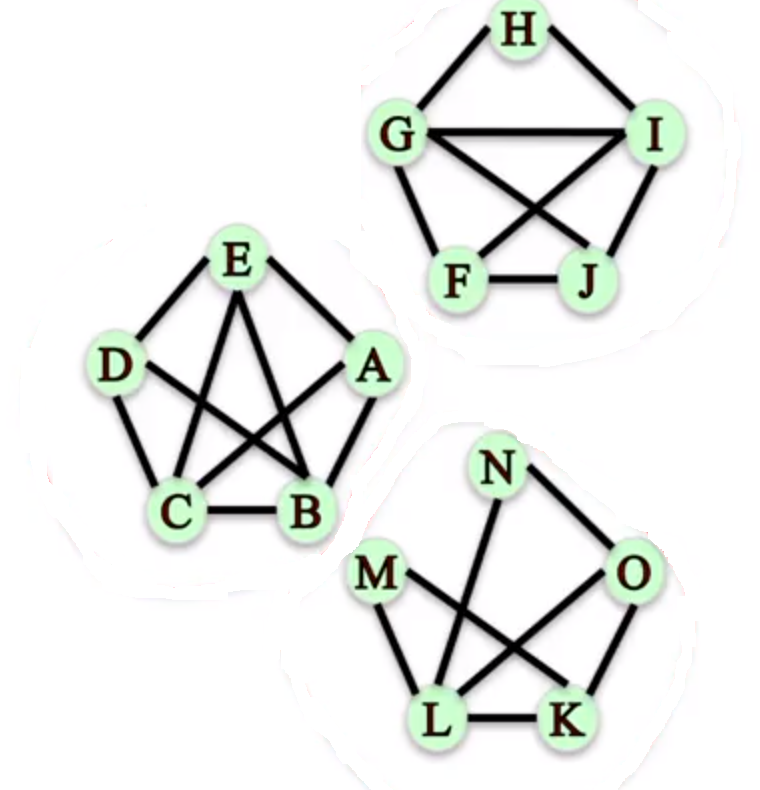
这里着重介绍一下在 Directed Graph 中的两种判断是否为联通图的方式

  • 1. 强联通图：每个节点 u 可以到 v，v 也可以到 u。
  • 2. 弱联通图： 只需要 u 可以到 v 即可，可以想象成，满足的条件就是将有向图变成无向图之后是强链接的即可。

Network Robustness

图的稳定性表现在，如果我移除任意节点，或者移除任意边，这个图的连接性是否仍然可以保证连通性。

图的稳定性分析在一些场景中非常有用，举个栗子，比如我们有一个航班图，我们需要分析如果某一个机场意外关闭，或者某一个航班意外取消，这会不会影响出行。 所以图的稳定性分析实际上描述的是一个图抵抗攻击的能力。同样的应用场景还有，电力网络，互联网攻击等。

那么如何定量的描述一个网络的稳定性呢，两个指标：

  • 1. 断开一个网络需要的最少的 Node Cuts
  • 2. 断开一个网络需要的最少的 Edge Cuts

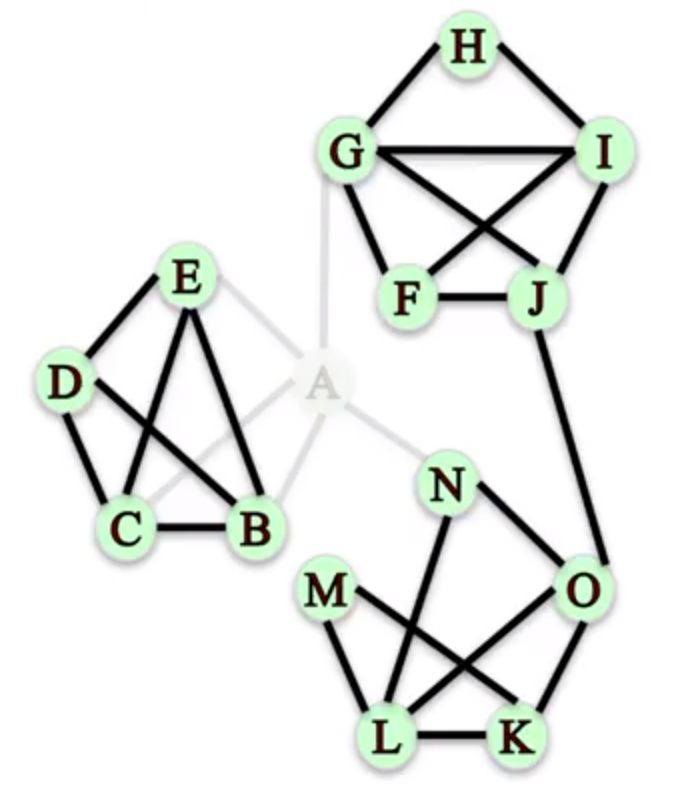
如上图所示，如果我们移除网络中的 A 节点，这个网络就会断开。

除了断开一个网络，有的时候我们也需要分析 A 节点到 B 节点之间的连接的稳定性，分析链接的稳定的指标也非常类似以上：

  • 1. 断开两个节点的链接需要的最少的 Node Cuts
  • 2. 断开两个节点的链接需要的最少的 Edge Cuts

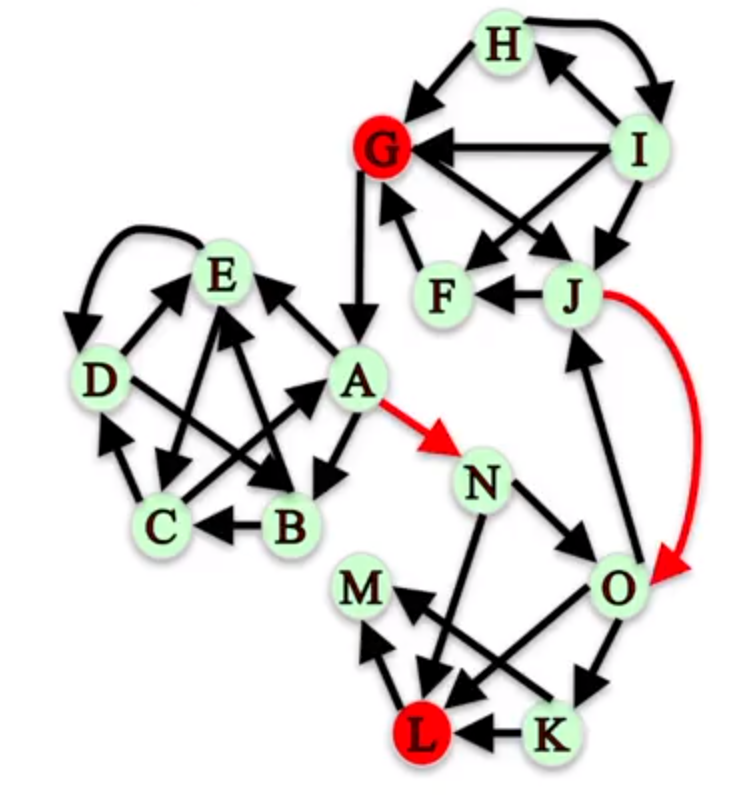
如上图所示，如果我们移除网络中的 A -> N 和 J -> O 连接，G -> L 的连接将会断开。

Summary

这篇博客一共介绍了图分析的四个方面：聚类系数，节点距离，联通子图和图和稳定性分析。并给出了相对应的参数来定量描述这些指数。他们会对应着不同的应用场景。