有人在我微信分享下来回复说想让我写梯度下降算法啦,哈哈,开心,说明我写的东西是有观众的,而且还是能帮助到一些人的。那么这篇文章我一定好好写,不负所托。
梯度下降,可以说是深度学习的基础中的基础了,前向传播,搭建网络框架,后向传播,梯度下降训练,就成了一个神经网络的全部过程。
梯度下降的算法有很多,这里,我不会将所有的算法都涉及到,但这里所谈到的优化器算法,可能是做深度学习的,一定得要知道的算法了。

据说,前面放动图,会更吸引人?
-> . <-
What is Gradient Desecnt ?
那么,什么是梯度下降呢?学习机器学习的同学们常会遇到下面这样的图像, 这个图像看上去好复杂, 不过还挺好看的,= . =。在这张图上我们做的事情是,从某一个随机的点出发,一步一步的下降到某个最小值所在的位置。
对于人来说,我们是很容易知道那条路径下降最快的,可是机器却不是那么聪明的。他们只能靠算法,找到这个最快下降的路径。这个算法,就是我们所说的梯度下降了。
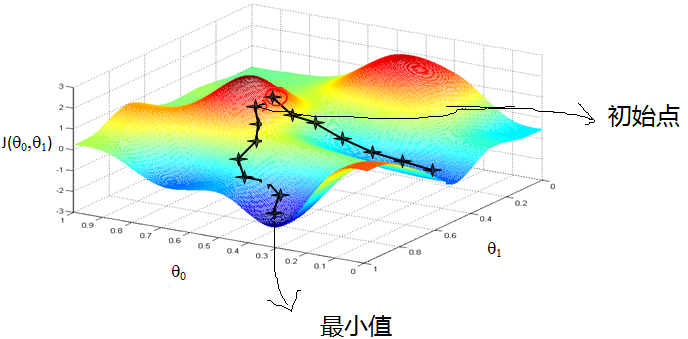
其实梯度下降只是一个大的问题家族中的一员,这个家族的名字就是 - ”optimization” (优化问题)。优化能力是人类历史上的重大突破, 他解决了很多实际生活中的问题。从而渐渐演化成了一个庞大的家族.比如说牛顿法 (Newton’s method), 最小二乘法(Least Squares method), 梯度下降法 (Gradient Descent) 等等。而我们的神经网络就是属于梯度下降法这个分支中的一个。
提到梯度下降, 我们不得不说说大学里面学习过的求导求微分。因为这就是传说中”梯度下降”里面的”梯度” (gradient)啦。听到求导微分,大家不要害怕, 因为这个博客只是让你有一个直观上的理解, 并不会涉及太过复杂的数学公式推导哈。
Accelerate Gradient Desecnt
越复杂的神经网络, 就会需要越多的数据来训练, 导致我们在训练神经网络的过程中花费的时间也就越多。我们不想花费这么多的时间在训练上. 可是往往有时候为了解决复杂的问题, 复杂的结构和大数据又是不能避免的,这就让人很抓狂了。

所以我们(迫切的)需要寻找一些方法, 让神经网络聪明起来, 下降的速度快起来。常见的加速模式有以下几种:
- Stochastic Gradient Descent (SGD)
- Momentum
- AdaGrad
- RMSProp
- Adam
Stochastic Gradient Descent
随机梯度下降,应该是最基础的一种加速算法了,Gradient Descent 利用全部数据,来计算梯度下降的方向,这肯定是能找到最优的下降方向,但是同时也造成了计算量过大,时间过长的后果。
我们换一种思路, 如果把这些训练数据拆分成小批小批的, 然后再分批不断放入 NN 中计算, 这就是我们常说的 SGD 的正确打开方式了. 每次使用批数据, 虽然不能反映整体数据的情况, 不过却很大程度上加速了 NN 的训练过程, 而且也不会丢失太多准确率.
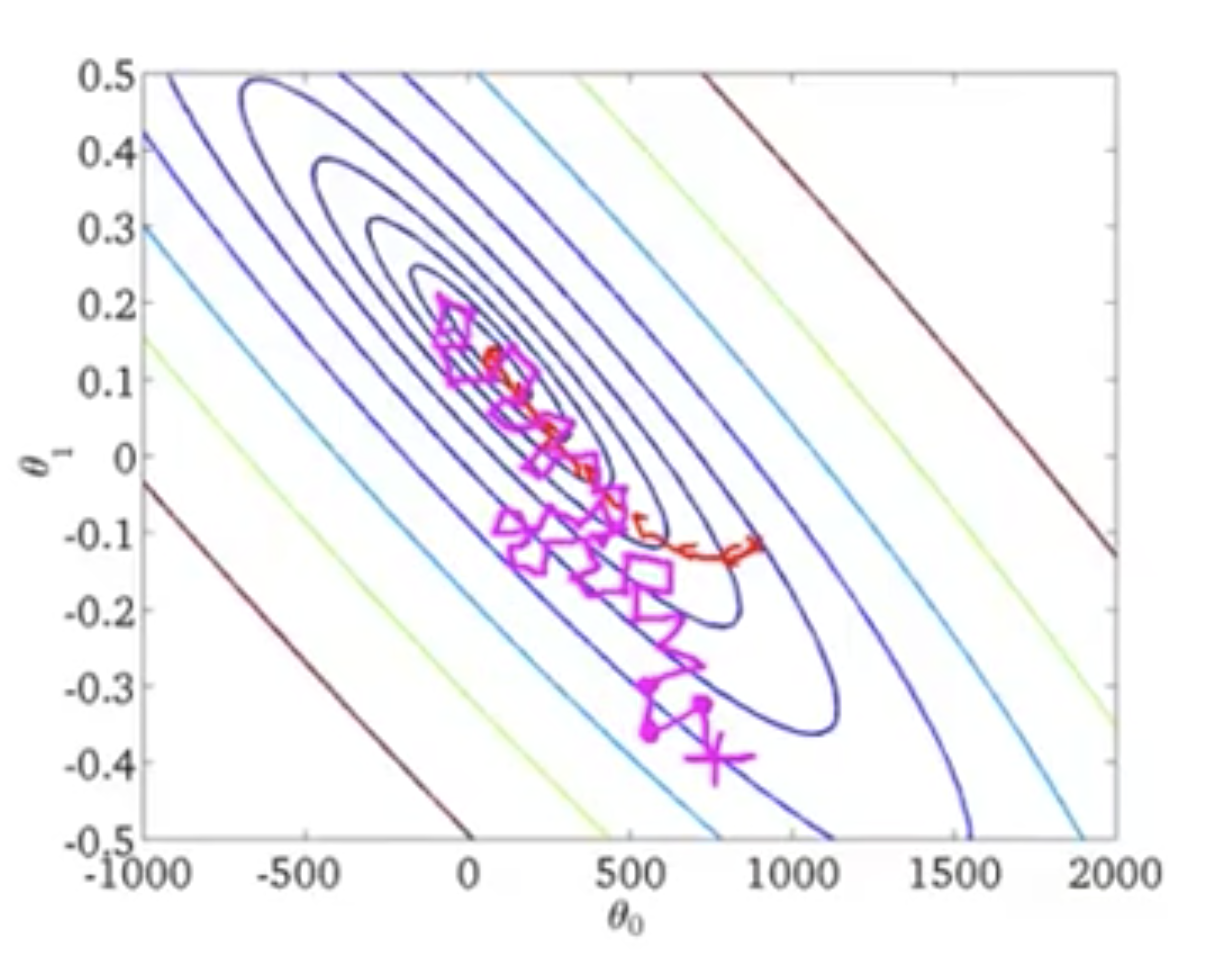
例如,上图中,如果我们是梯度下降的话,我们每一步都会走最正确的下降方向,不会走弯路,那就是图中红色线所表示的走法,如果是随机梯度下降的话,就是紫色线路所代表的走法,他可能会绕一些弯路,但是扭扭曲曲,却还是能朝着最小值的地方走过去。
注意,往往随机梯度下降,不会刚刚好就找到最小的地方,可能会在最小值附近转来转去的。
Momentum
如果说在训练的时候,我们觉得随机梯度下降 SGD 算法依然太慢了,怎么办呢?这时,我们就可以考虑使用 Momentum 了,Momentum 算法它是可以帮助到快速的梯度下降的。
在真正进入到算法讲解之前,我们先来大致看一下,在大多数训练的过程中,那些曲折无比的学习过程吧。
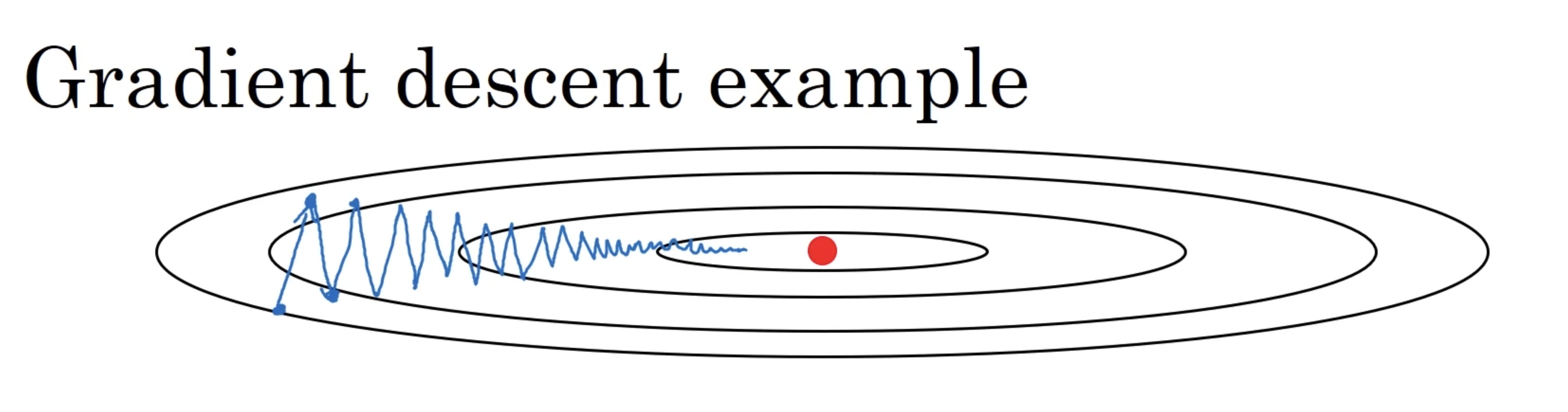
例如上图中的梯度下降的例子,这个梯度下降的过程,很像是在某一个轴附近摆来摆去,虽然确实是一直朝着中间的洼地在走着,但是好像来回的摆动确实是浪费了许多步骤,看上去像一个喝醉了的人,晃晃悠悠的向着地低走去。
实际上,由于真实的训练过程中,维度远比 2 要高的多,这种无意义的摆动的情况出现的情况,出现的次数非常多。
那么 Momentum 就是发现了这种问题,对 SGD 算法做了一些改进。一句话来概括它的特点的话,那就是:计算在梯度下降的方向上,计算一个指数加权平均( Exponentially weighted average ),利用这个来代替权重更新的方法。
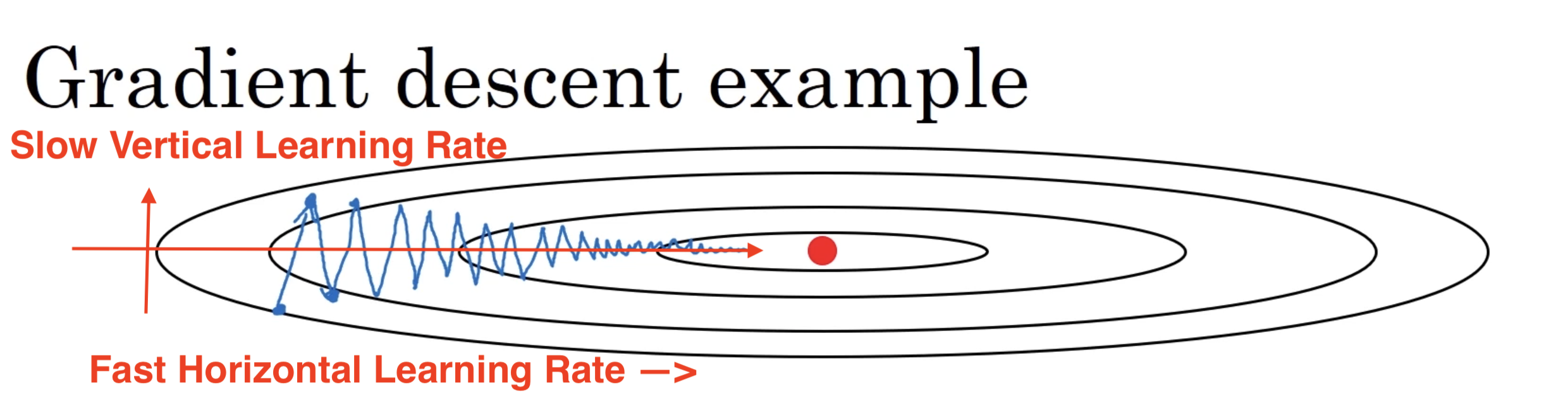
用通俗一点的方法来说,就是“如果梯度下降显示,我们在一直朝着某一个方向在下降的话,我让这个方向的的学习速率快一点,如果梯度下降在某一个方向上一直是摆来摆去的,那么就让这个方向的学习速率慢一点”。
我们可以先来看一下,Momentum 减少摆动的效果。
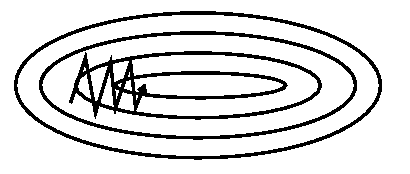
没有 Momentum 的 Gradient Descent
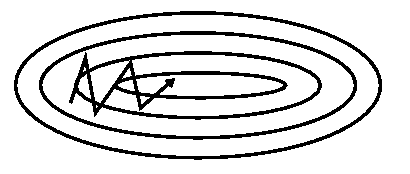
有 Momentum 的 Gradient Descent
上面两张图,就是我们没有加入,和加入了 Momentum 之后的梯度下降的变化,可以看到,有了 Momentum 之后,算法加速了横轴下降的速度,并减缓了纵轴的摆动的频率,所以在最终的训练过程中,它的步伐迈的更大,也更正确了,对比原来没有 Momentum,仅仅四步,就离最终的最小值更近了许多。
Exponentially Weighted Average
如果你只是想知道 Momentum 的大致原理,不想知道 Momentum 的细节的话,那么这一部分你是可以跳过的啦。
前面我们提到,Momentum 是用到滑动平均来获得平滑波动的效果的。那么什么是滑动平均呢?
滑动平均实际上是一种用来处理“数字序列”的方法,你们玩的股票里面的各种多少天的线,周线,月线,年线,等等,都是这种方法弄出来的。具体是怎么做的呢?假设,我们有一些带噪音的序列的序列 S。在这个例子中,我绘制了余弦函数并添加了一些高斯噪声。它看起来像这样:
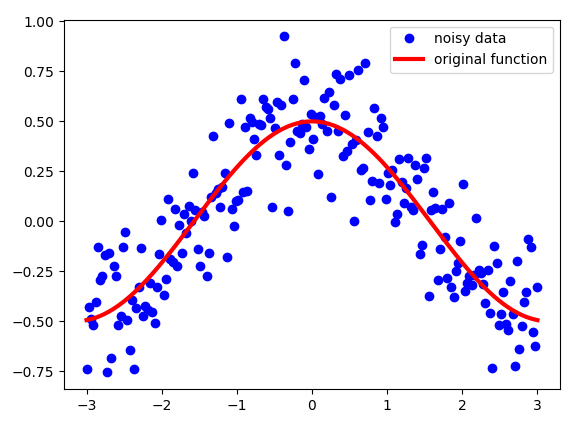
请注意,即使这些点看起来非常接近每个点,但它们都不共享 x 坐标。这是每个点的唯一编号。这是定义我们序列 S 中每个点的索引的数字。
我们想要对这些数据进行处理,而不是使用这些数据,我们需要某种“移动”平均值,这会使数据“降噪”并使其更接近原始功能。指数平均值可以给我们一张看起来像这样的图片:
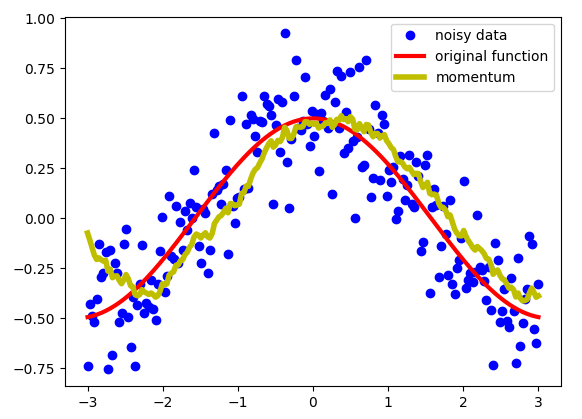
正如你所看到的那样,这是一个相当不错的结果。我们得到了更平滑的线条,而不是具有很多噪音的数据,这比我们的数据更接近原始功能。指数加权平均值用以下等式定义新的序列 V :

序列 S 是我们原始的带噪音的序列,序列 V 是我们经过滑动平均得到曲线,也就是上面绘制的黄色。 Beta 是一个从 0 到 1 的超参数。上面的 beta = 0.9。这是一个非常常用的值,最常用于带 Momentum 的 SGD。我们对序列的最后做 1 /(1- beta)进行近似平均。
让我们看看beta的选择如何影响我们的新序列 V 的吧。
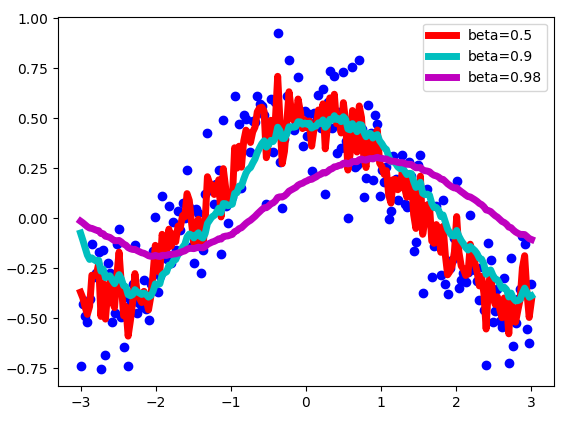
正如上图所示,beta 值越大,曲线与含有噪音的值越接近,beta 越小,曲线越平滑。
接下来,我们来一波数学公式推导吧。

如果我们一步一步的将生成新序列的方程展开的话,就会发现是这样的关系。

将下面的公式一步一步带入上面。
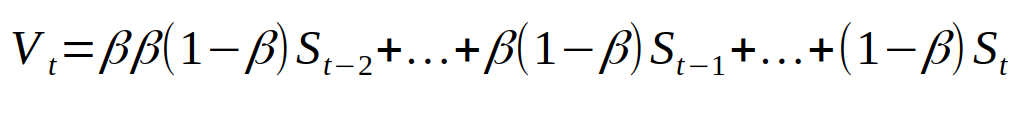
然后再简化一下。就得到了这样的东西。
简单说一下上面公式的意义吧,如果你不想看公式的话,其实就是说,生成的新序列,离得越近的数据,对它的影响越大,离得越远的数据,因为 beta 已经被乘了好多次方了,所以影响就小了许多,这也就是 Exponentially (指数)滑动平均的意义所在。
Why Momentum Works ?
我们已经定义了一种方法来获得某个序列的“移动”平均值,而且这种平均值会与数据一起变化。那么我们如何将它应用于训练神经网络呢?
这里,我给出 Andrew Ng 在 coursera 的 Deep Learning Specialisation 中的定义。他的解释 Momentum 的方式是,我们定义了一个动量,这个动量 Momentum 就是我们渐变的移动平均值,它会取决于前面的梯度下降的值的大小。然后我们用它来更新网络的权重。这可以写成如下:
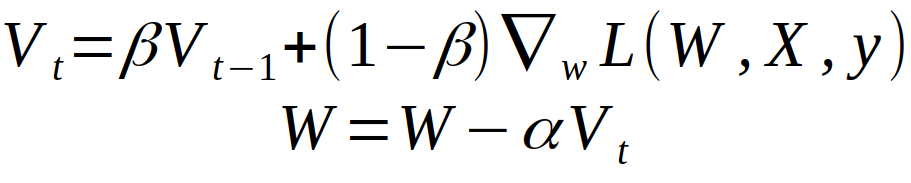
上图中的 L 是 loss function,倒三角形状的东西,是梯度,alpha 是学习速率,beta 就是控制我们滑动平均的平滑指数的一个参数。

那么从数学公式的角度上来说,Momentum 为什么是可以达到加速的效果的呢。请记住一点就好,Momentum 带有了滑动平均,滑动平均会将上下浮动的噪音式特征抹去,也即是我们在上图中看到的摆来摆去的动作幅度,就被滑动平均给抹平啦,但是如果你一直在朝着某一个方向走的话,滑动平均是抹不平的,
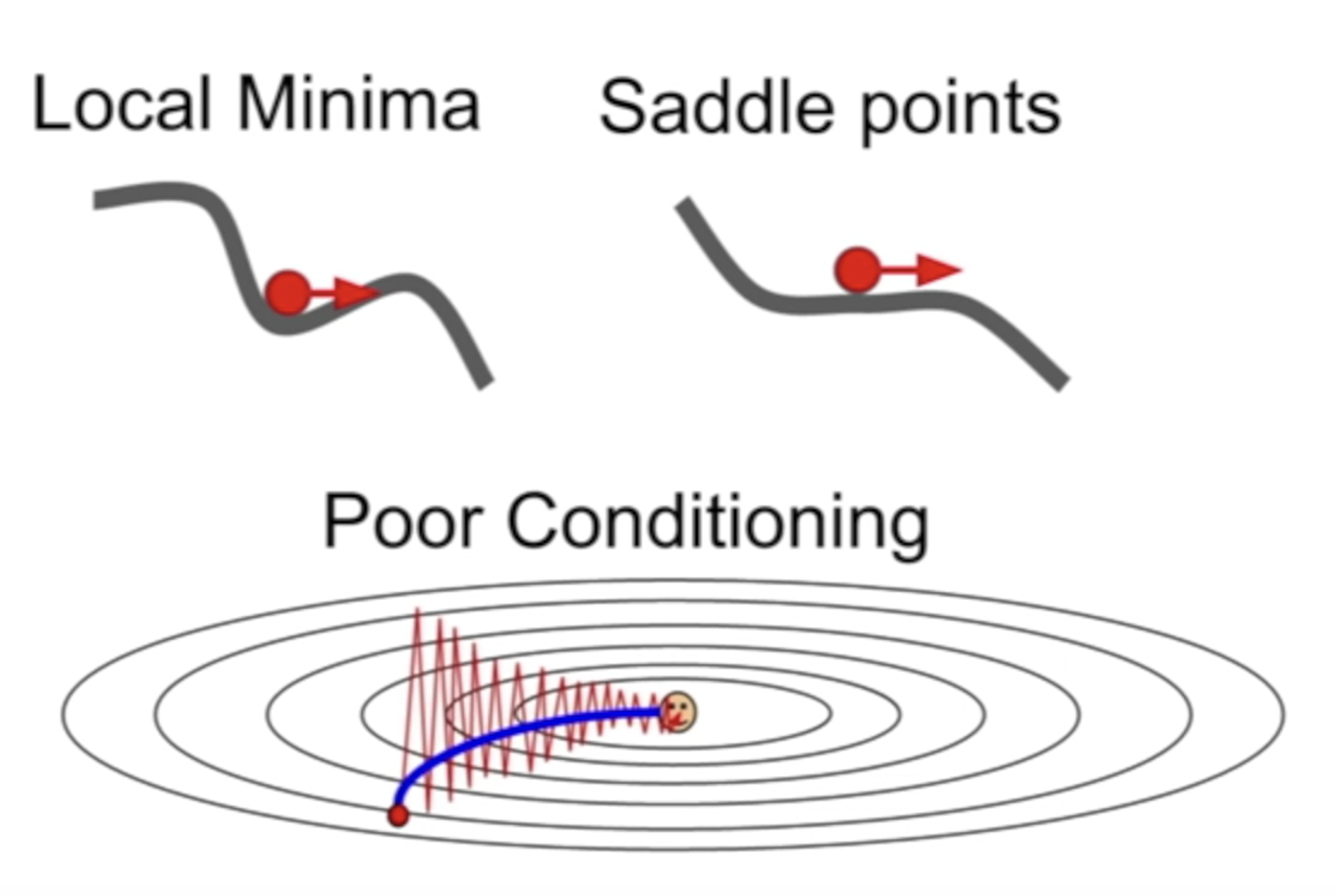
Momentum 还有一个好处,就是可以冲出局部最优解,或者某一些梯度为 0 的地方,这也是因为滑动平均使他带有一定的惯性,能冲出洼地。
Nesterov Accelerated Gradient
Nesterov Momentum 是一个稍有不同的 Momentum 更新版本,最近很流行。在这个 Nesterov 中,我们首先查看当前动量所指向的点,然后计算此时的梯度。如下图所示

Nesterov Momentum 的计算公式可以表示为:
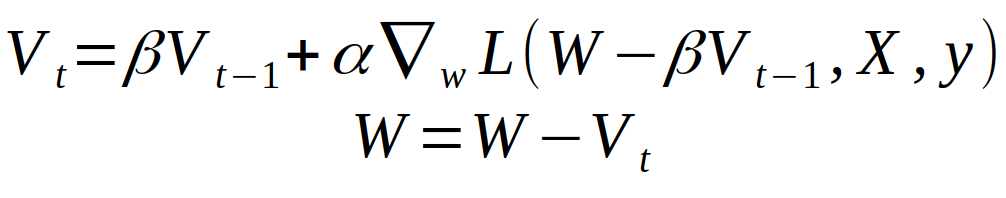
它唯一的区别是 W 变成了 W - Vt,但这里我并不打算细说 Nesterov Momentum 了,我们直接来看一个梯度下降的对比图吧。

可以看出 Nesterov Momentum 比单纯的 Momentum 要少走了许多弯路,更直接的走向洼地。
AdaGrad
AdaGrad 是另外一种非常常见的梯度下降的优化方法,他的主要思想就是,在比较晃荡的下降方向上,给予一定的阻力,让你不要那么的晃,晃得越厉害,就阻力越大,导致你不能晃。具体的做法,我们看一下 AdaGrad 的计算方法来说明吧。

首先,在梯度下降的方向上,我们会有一个变量 grad_squared 存储在该方向上的变化的平方的累积,也就是说,如果在这个方向上,如果波动一直很大的话,这个 += 操作会让这个方向上的 grad_squared 越来越大,相对应的,而如果变化一直很小,这个方向上,不怎么晃的话,grad_squared 也会一直比较小。
注意,这里的看上去是变量的东东,实际上都是 vector 哈,numpy 的乘法和除法,都是对每一个元素进行的,而不是我们传统意义上的向量点乘。

记下来,在计算梯度变化的时候,我们会额外的除以一个因子,这个因子是用来操控梯度下降真实的变化大小的,即是说,按照公式,如果前面的 grad_squared 累积的越大,那么在该方向上,除数就越大,导致在这个方向上,后来就很难移动了,同理,前面的累积越小,在这个方向上,梯度的变化也就越大。
形象的来说,AdaGrad 的作用和 Momentum 类似, 不过 AdaGrad 不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走。
Problems With AdaGrad ?
细心的同学不难发现,AdaGrad 是很明显的存在着一个问题的:
- grad_squared 是一个一直累积的过程,那么积少成多,哪怕是在一些方向上,它的波动一直很小,但是由于是不停的迭代增加, grad_squared 最终也会变得很大,导致在训练的后期,任意一个方向上,都有着很大的阻力,梯度下降就走不下去了。
RMSProp
RMSProp 基于 AdaGrad,进行了一些小小的改动,也解决了我们上面提出来的,在随着训练时间增长,AdaGrad 的步伐会变得很小的问题。RMSProp 的做法是这样的:
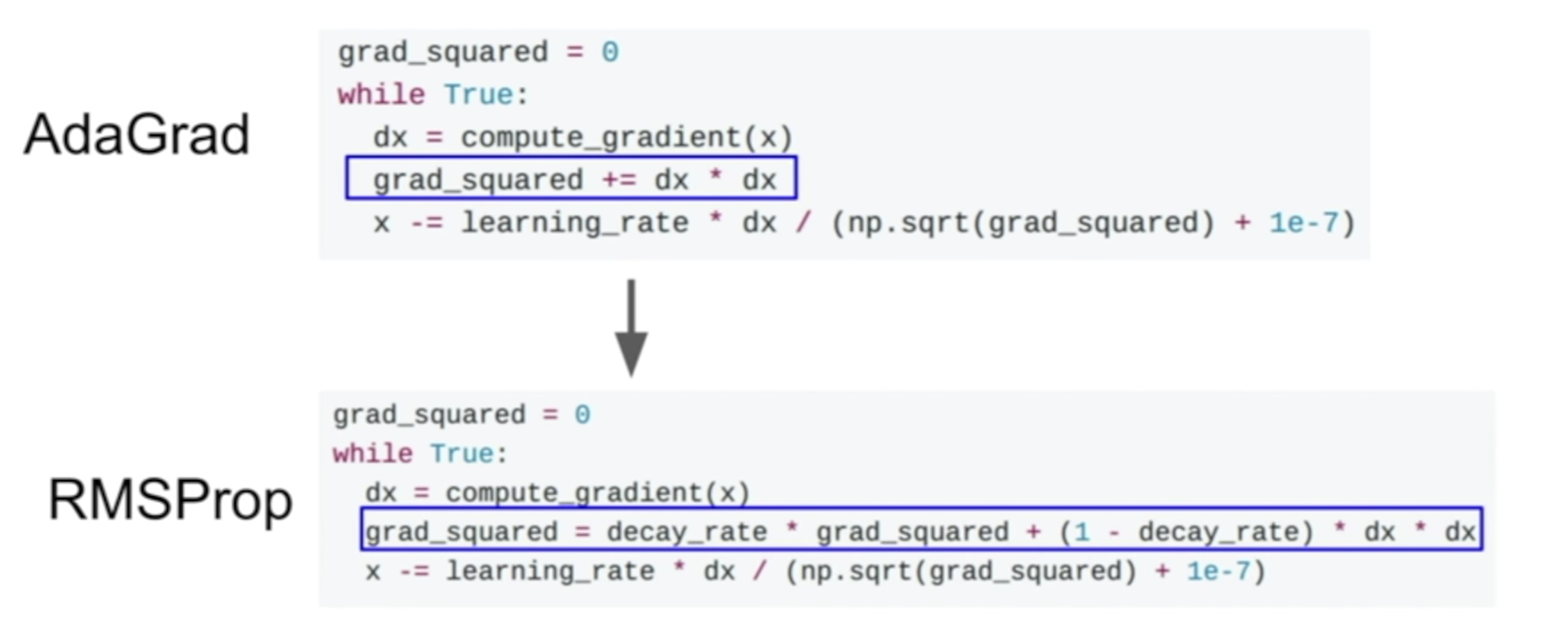
简单对比一下 RMSProp 与 AdaGrad ,会发现 RMSProp 在计算 grad_squared 的时候,加上了一个 decay (衰减率)的东西,这样造成的效果即是,既保留了 AdaGrad 的特性,又不会一直过分增加 grad_squared 导致最后阻力过大。

如果我们对比一下 RMSProp 以及 Momentum 的下降效果,会发现 Momentum 由于带着冲量,走的很快,往往是先走过头了,然后再走回头路,找到最终的最优化的位置,而 RMSProp 则是在走的过程中,不停的在调节着自己,朝着最正确的地方走去。
Adam
实际上,前面的梯度下降的优化方法,我们是有两种思路的,一种是 Momentum 派系,他们的思想就是,让下降带冲量,另一种是 AdaGrad 派系,他们的思想则是波动太大,就给你阻力,防止你波动。这两种思想都非常不错,那有没有可能,将两种思想结合到一起呢?答案是有的,那就是 Adam。

如上图所示,红色部分来自于 Momentum,蓝色部分来自于 RMSProp。那么这种非常 naive 的合并两个算法,会不会有问题呢?
考虑一下在我们梯度下降的第一步的时候,会怎样。看 second_momentum,由于最开始的初始化的时候,second_momentum 是 0,且beta2 的值,我们也一般会设置成 0.99 这样的比较接近 1 的值,就会导致 second_momentum 在第一步的时候,值会非常的小。在最后算梯度更新的时候,如果除以这么一个很小的值,那么第一步的步伐会变得很大。
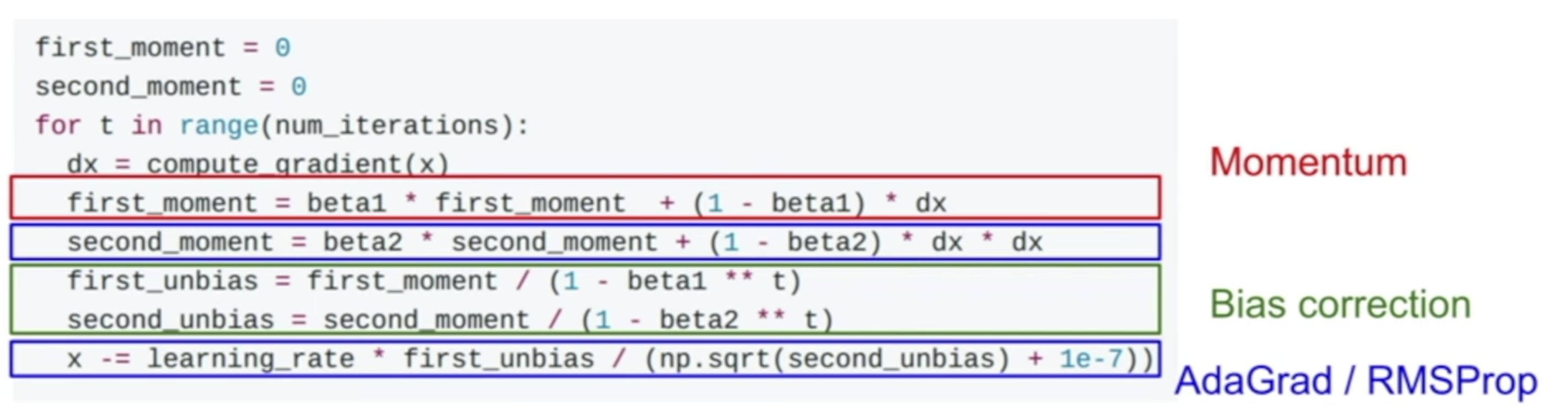
我们知道最开始的步伐太大,不是很好,所以 Adam 在处理的过程中,加入了一定的 bias,这样的话,就可以防止最开始的时候步伐过长了。
通常,我们会选择 0.9 作为 beta1 的值,0.99 作为 beta2 的值,1e-3 或者 5e-4 作为 learning rate。这些参数对于绝大多数的模型都能取到不错的效果。
如果我们这个时候,对比一下 Adam 与其他的梯度下降的算法的话,会发现 Adam 实际上是中和了前两种的,速度比较快,也不容易走偏。
Visualization of Algorithms
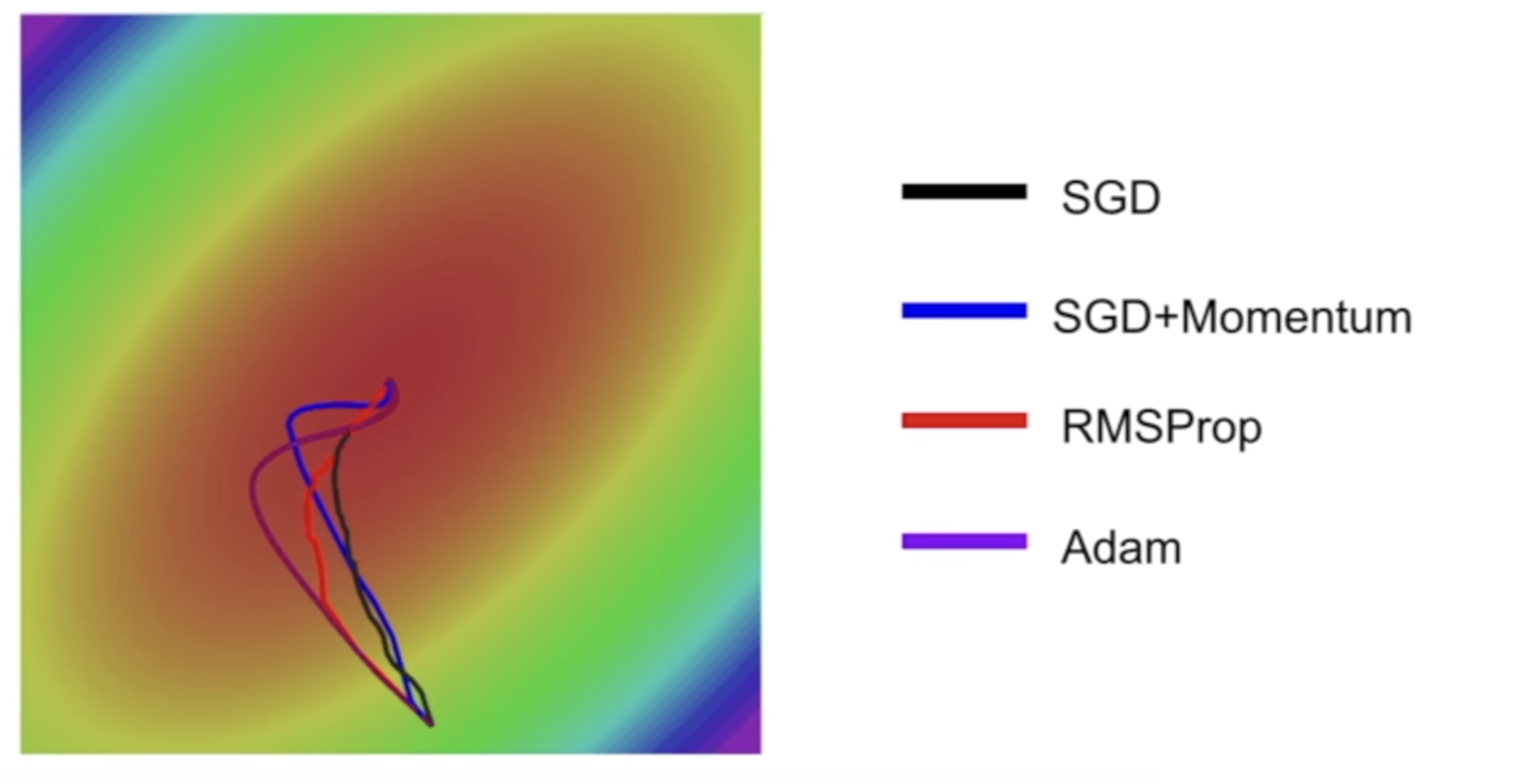
下面这个动画(图片来源:Alec Radford)为大多数所提出的优化方法的优化行为提供了一些直觉。在这里也可以看看Karpathy对同样图像的描述,以及所讨论算法的另一个简要概述。
这张图也算比较老的图了,有一些里面涉及的算法我在这篇博客里没有提到,而我提到的 Adam 它也没有画出来,所以将就着看一下吧。

这里可以看到的是 Momentum 系的梯度下降方法,像一头脱缰的野马一样,虽然速度很快,却很容易冲过头了,AdaGrad 系的速度虽然慢一些,但是却一直在不断调整自己,往着正确的方向在走。而 SGD 则像一个勤勤恳恳的老牛,每次都走着正确的方向,却慢的要死。这里补充一下 Adam 的下降速度和方向,大概就是介于 Momentum 和 AdaGrad 系之间。
Which Optimizer to Use ?
最后的最后,我们来简单说一下,我们应该使用哪个优化器吧?如果我们的输入数据很稀少,那么可能会使用自适应学习率方法中的一种,来获得最佳结果。这样的一个好处是,我们不需要调整学习速率,它可能就会达到默认值的最佳结果。
自适应学习率方法中,RMSprop 是 AdaGrad 的延伸,它解决了其学习速度急剧下降的问题,Adam 最后为 RMSprop 增加了偏差修正和动力。就此而言,RMSprop 和 Adam 是非常相似的算法,在相似的情况下,Kingma等人表明,偏差修正有助于 Adam 在优化结束时略微优于 RMSprop ,因为梯度变得更加稀疏。就目前而言,Adam 可能是最好的整体选择。
一个比较有意思的事情是,看似最不好的 SGD 下降方法(因为它花费的时间最长),有时却能达到最好的学习效果。如果想要做到这一点,我们需要三个重要的地方下额外的功夫:
- 1. 一个非常好的初始值的设定。
- 2. 学习速率的 decay
- 3. 类似于模拟退火算法的让梯度下降不要卡在鞍部
当然,如果你不想要这么复杂的话,Adam 应该能满足你的需求了。