上一篇博客介绍了 GoogLeNet, GoogLeNet 有一个另外的名字,叫做 Inception-v1,那么既然有 v1,肯定就会有一个系列紧随其后,这篇博客首先介绍一下 Inception 系列的进化过程,和另外一个牛逼哄哄的网络 ResNet。
Inception-V2(Sergey Ioffe,2015)
不得不说,谷歌的团队就是厉害,在 GoogLeNet 发明后,不停的对它进行改良,发表了一个又一个更加厉害的网络。
Inception-V2 是 GoogLeNet 的第一个改良版,与前一个版本相比,它的主要变化总结起来有两个:
-
1. 加入了 BN (Batch Normalization)层,增加了这一层的好处有:
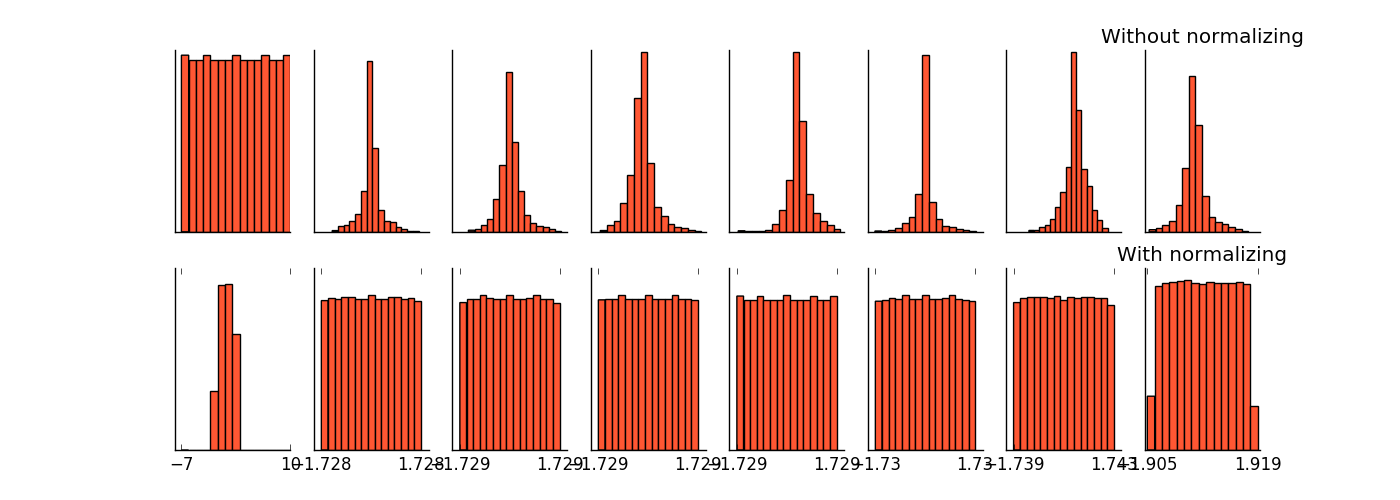
- 1. 1 减少了 Internal Covariate Shift(内部 neuron 的数据分布发生变化),使每一层的输出都规范化到一个 N ( 0 , 1 ) 的高斯。下图展示了加入了 Batch Normalization 和没有加入 BN 层的产生的权值分布的变化图。
- 1. 2 增加了模型的鲁棒性,可以以更大的学习速率训练,收敛更快,初始化操作更加随意。
- 1. 3 作为一种正则化技术,可以减少 dropout 层的使用。
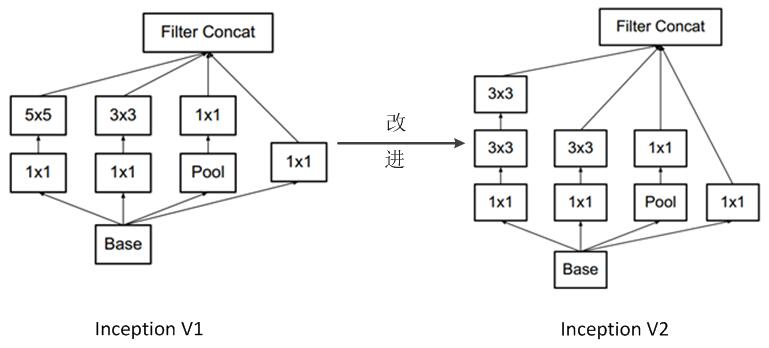
- 2. 用 2 个连续的 3 x 3 conv 替代 inception 模块中的 5 x 5,从而实现网络深度的增加,网络整体深度增加了 9 层,缺点就是增加了 25% 的 weights 和 30% 的计算消耗。
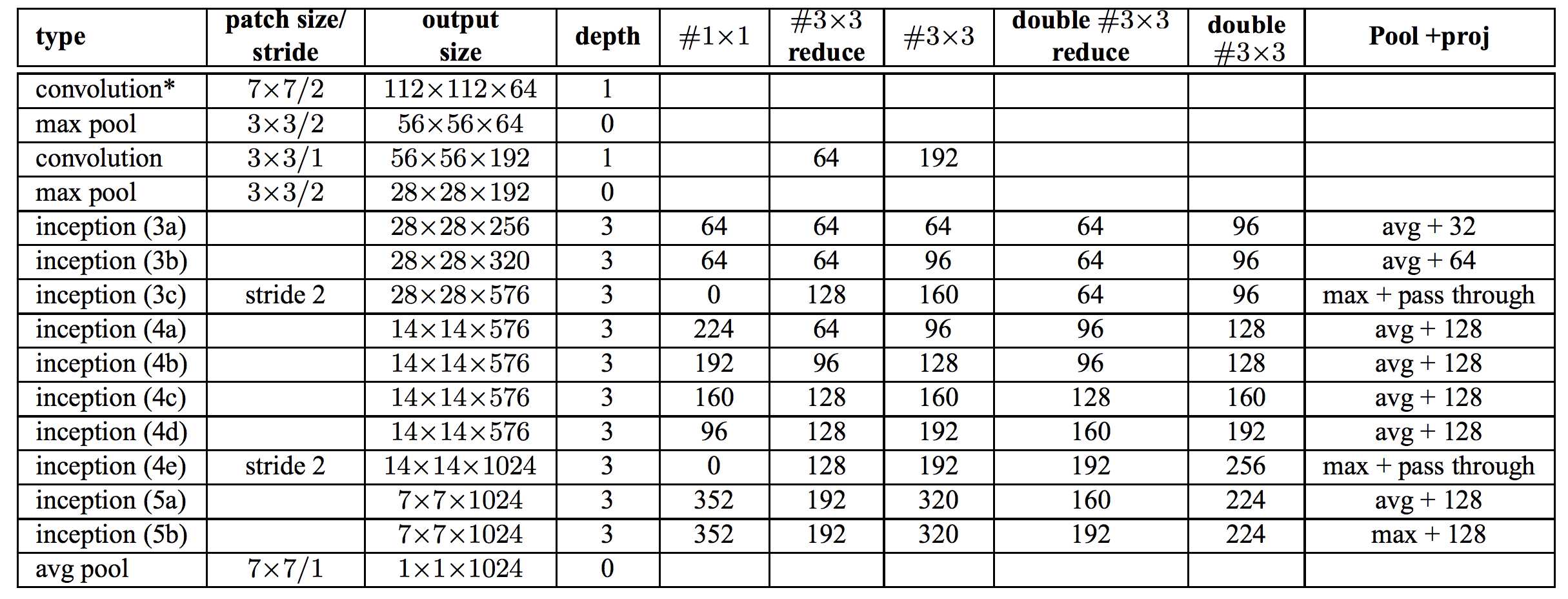
Inception-V2 的架构图如下
Inception-V3(Sergey Ioffe,2015)
Inception-V3 网络,主要在 V2 的基础上,提出了卷积分解(Factorization)的概念,为什么要提出这个概念呢?主要是为了在保持特征提取性能的同事,减少计算量。
那么卷积分解(Factorization),具体是怎么做的呢?看下面两个例子。
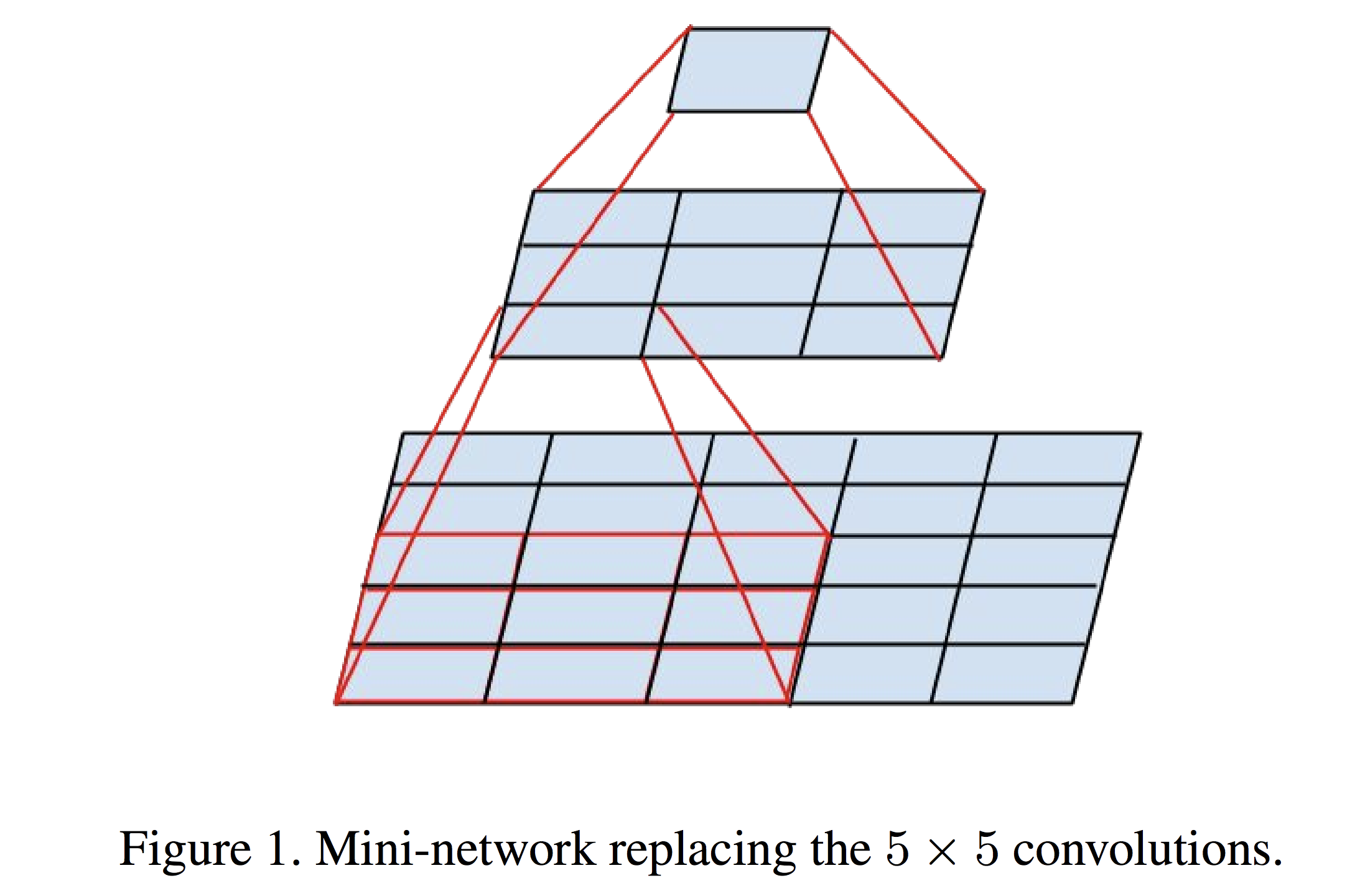
1. 对于 “ 大 ” 的卷积核,例如下图的 5 x 5 的卷积核,将其转换成两个 3 x 3 的卷积核,这样,需要计算的参数量就是之前的 18 / 25。
2. 对于 “ 小 ” 的卷积核,例如下图的 3 x 3 的卷积核,将其转换成 1 x 3 和 3 x 1 的卷积核,这样,需要计算的参数量就是之前的 2 / 3。这里需要注意的是,为什么不用两个 2 x 2 的卷积核来分解呢?原因是两个 2 x 2 的卷积核只能减少 1 / 9 的计算量。而 1 x 3 却能减少 1 / 3 的计算量。
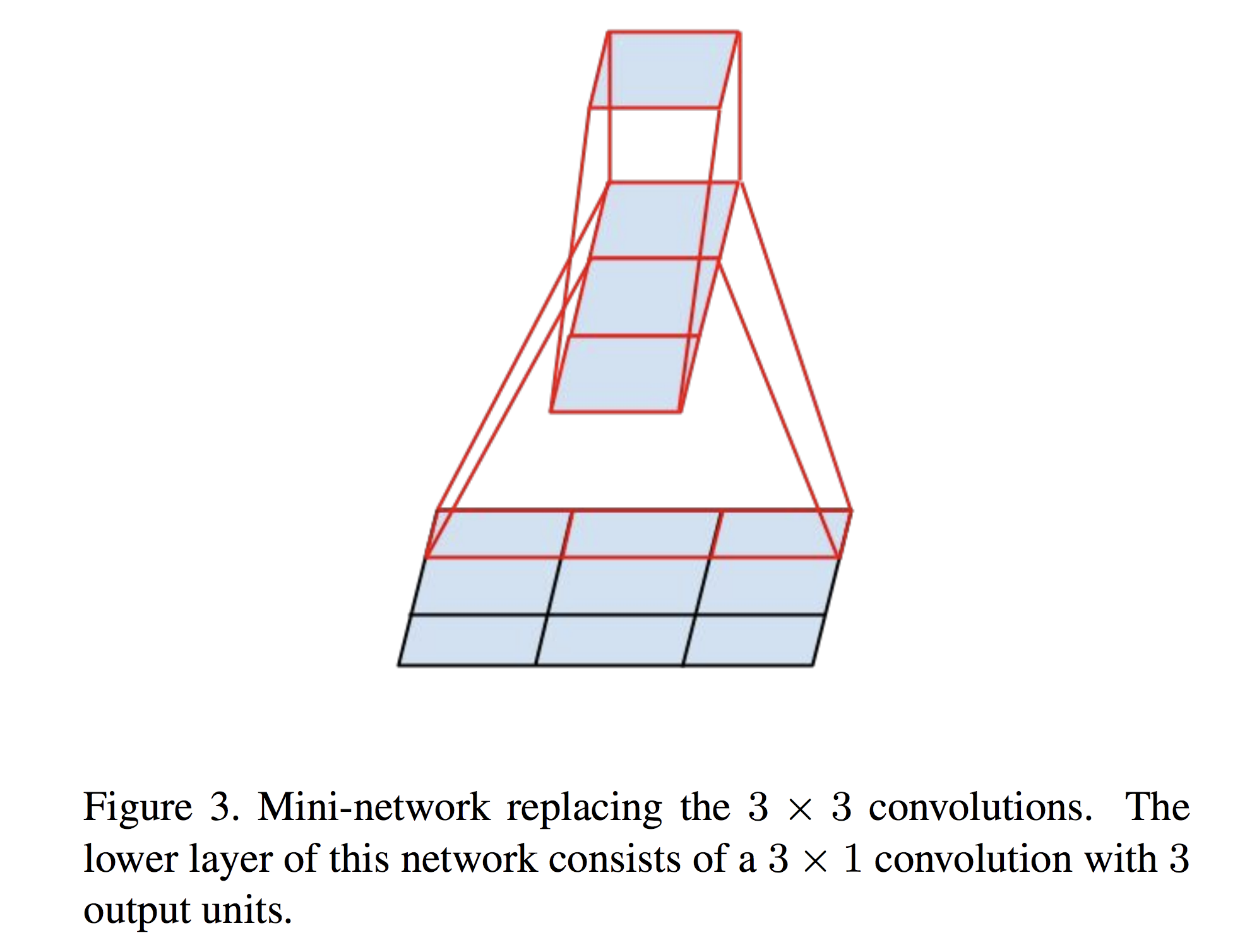
作者提出,在实际运用中,太早的时候用 1 x 3 和 3 x 1 的卷积核效果不好,所以在网络的前期,往往采用 1 x 7 和 7 x 1 的尺度。
好,回归正题,在 Inception-V3 中,卷积分解(Factorization)具体是怎么做的呢?其实在 V3 模型中,他们一共用到了 “ 三种 ” 不同的 Inception 的结构。对应在架构中的位置分别如下。
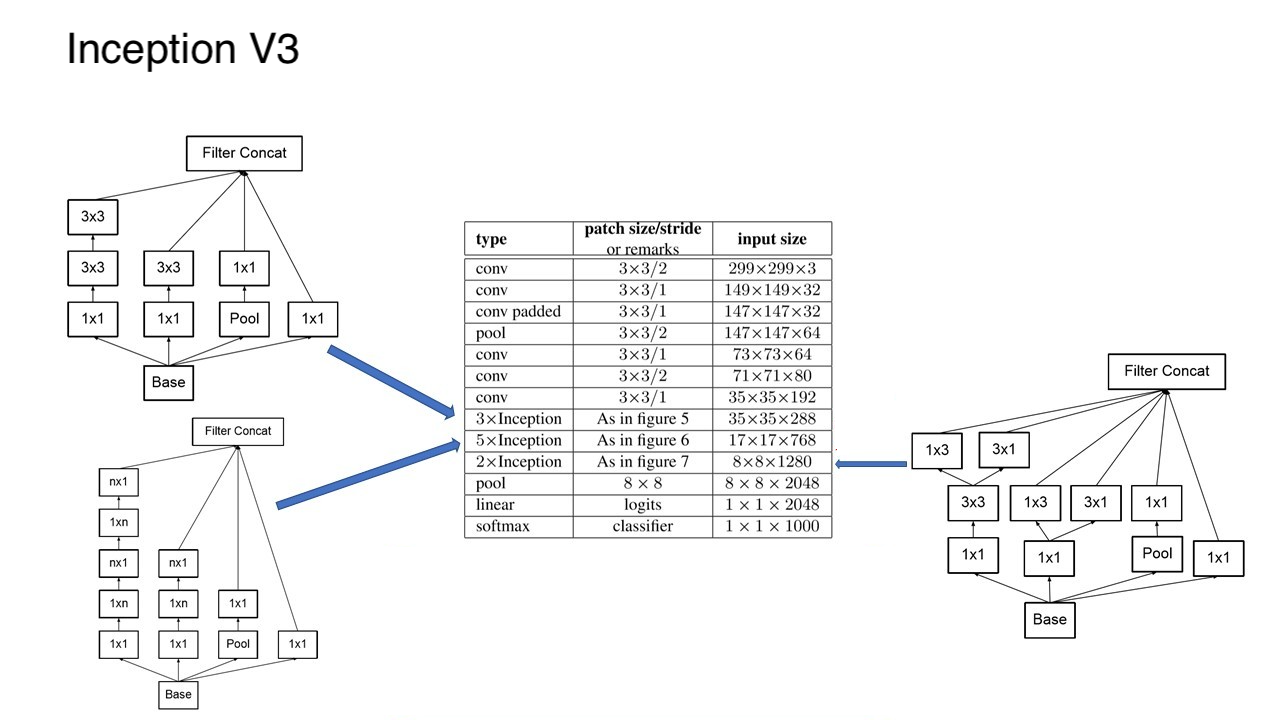
=> 第一个 Inception 和 V2 中的一样,只是将 V1 版本中的 5 x 5 卷积替换成了两个 3 x 3
=> 第二个 Inception 进行了横向和纵向的因式分解,将 n x n 分解成了 n x 1 和 1 x n。
=> 第三个 Inception 将 3 x 3 的卷积核进行了再次拆解。
为了进一步的减少计算量,在 Inception 层与层之间的结构,也进行了网格大小的优化。卷积网络通过池化层来减少特征图的 Grid Size,而交换卷积层和池化层的位置,可以减少计算量。例如:
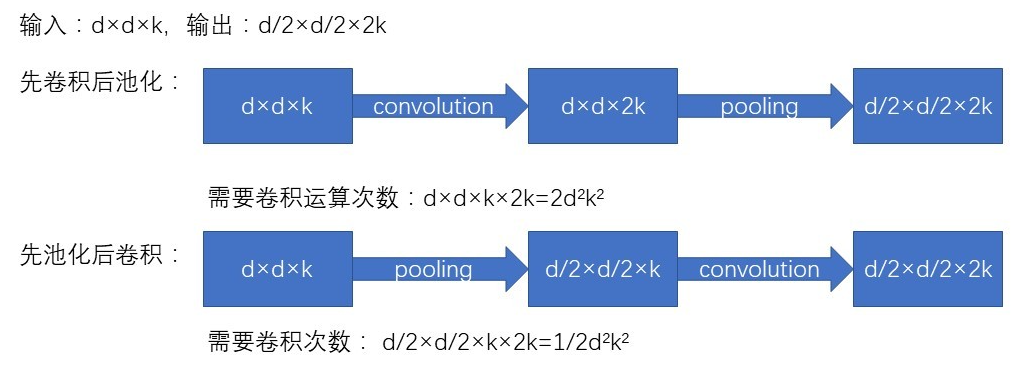
Inception V3 中对比了两种模型,他们的区别是,到底是先做 Inception 再做 Pooling 呢?还是先做 Pooling 再做 Inception 呢?
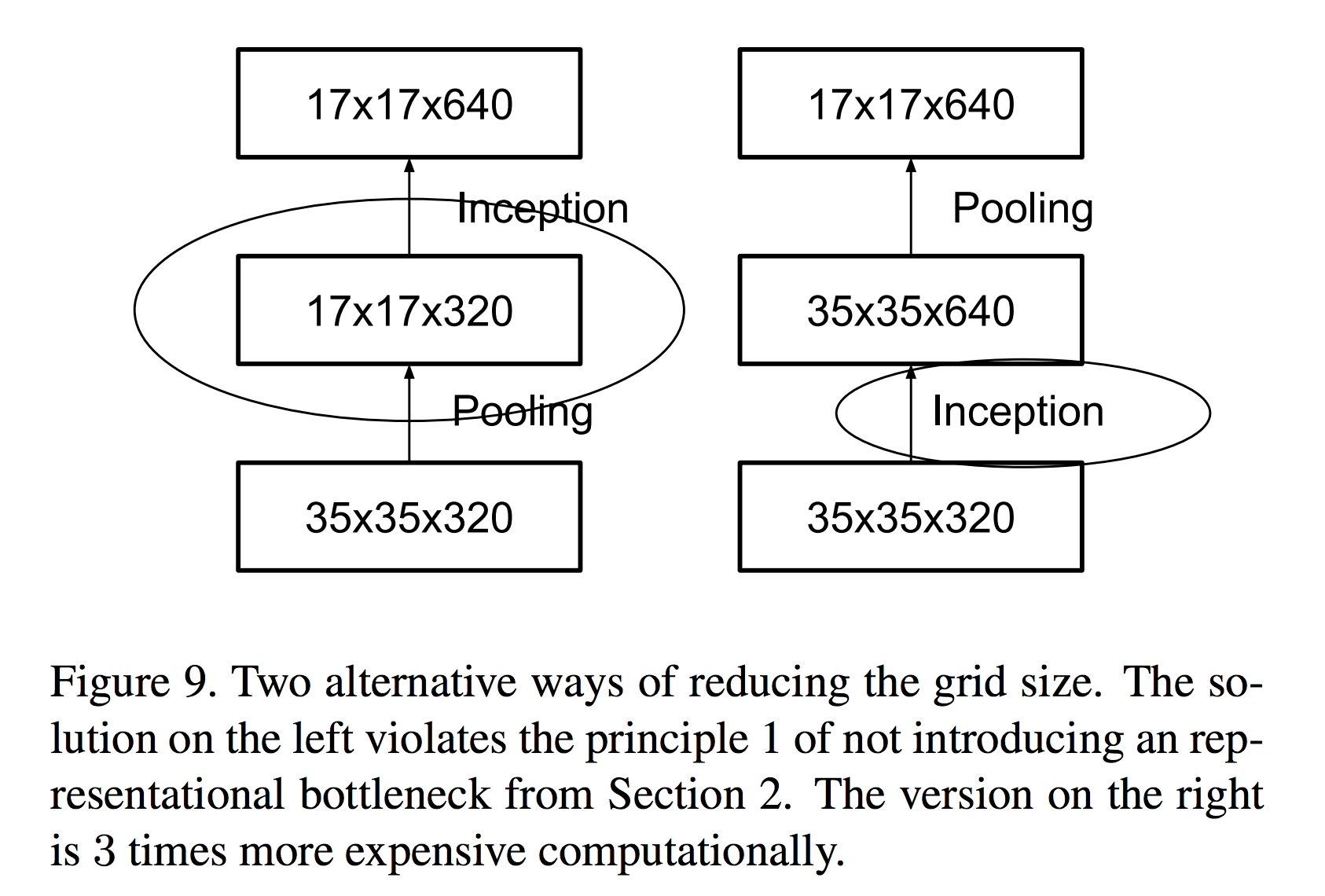
左边的做法,不满足 representional bottleneck 原则,即是,在网络的前期,不宜下降的太快。右边虽然满足了这个原则,但是计算量却是左边的 3 倍。
为了解决这个冲突,Inception-V3 提出了一个能同时满足两个优势的模型,如下图。

那么,加上这个层与层之间的连接模块,Inception-V3 的最终版本终于浮出了水面,它的最终结构如下图。
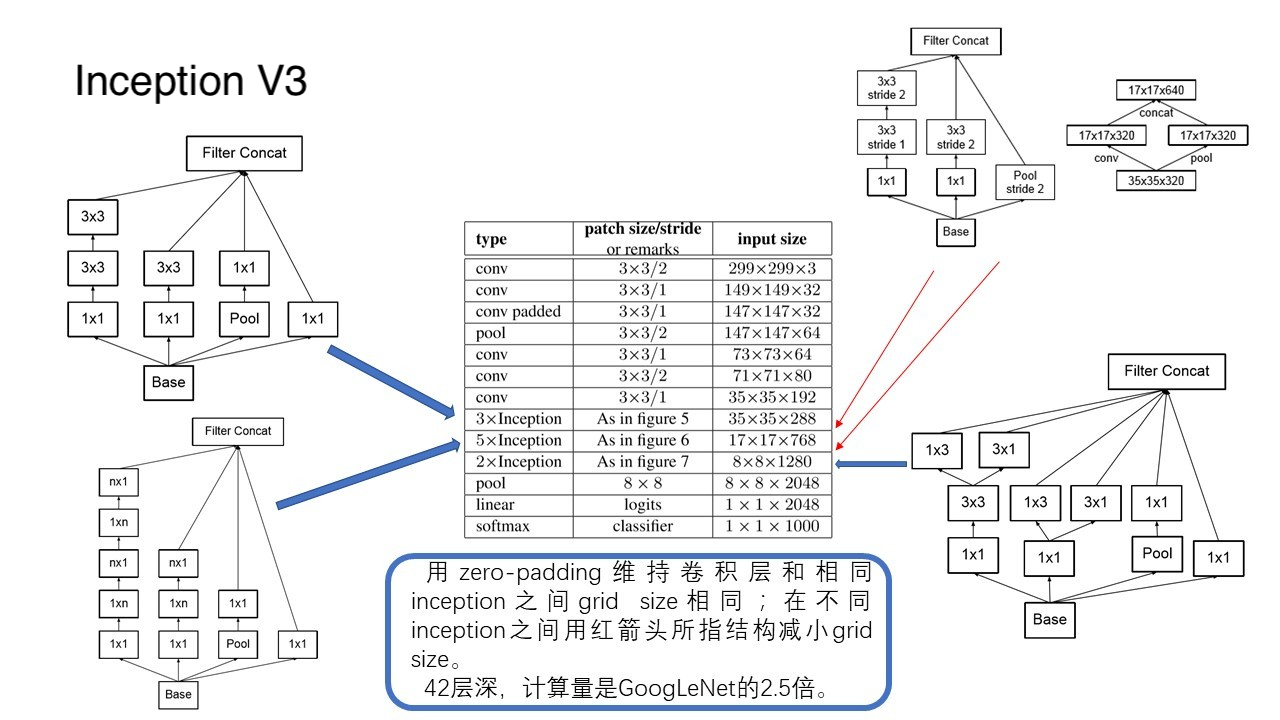
注意到,Inception-V3 相比于 GoogLeNet,层数达到了 42 层,是原来的 2.5 倍,已经深到作者都无法在 paper 中画出来了,只能靠粗略的简图概略结构了。(GoogLeNet 的论文中是有它的完整层次结构的。)
ResNet (Kaiming He, 2015)
这里先不介绍 Inception-V4, 因为要理解 Inception-v4 的话,必须要先弄明白 ResNet 的概念,因为实际上 Inception-V4 主要就是看到ResNet觉得挺好,就拿来和 Inception 模块结合一下,加 shortcut。
深度残差网络(Deep residual network, ResNet)的提出是CNN图像史上的一件里程碑事件,让我们先看一下ResNet在ILSVRC和COCO 2015上的战绩:
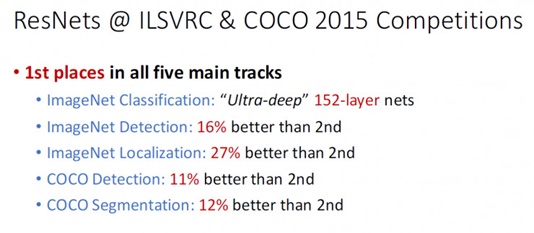
图1 - ResNet 取得了5项第一,并又一次刷新了 CNN 模型在 ImageNet 上的历史
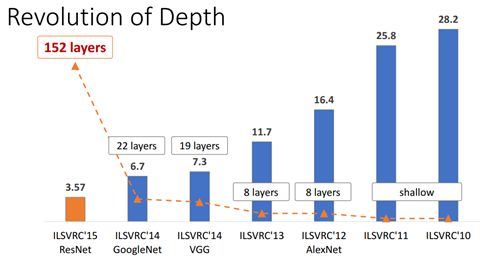
图2 - ImageNet 分类 Top-5 误差
ResNet 的作者何凯明也因此摘得 CVPR2016 最佳论文奖,当然何博士的成就远不止于此,感兴趣的可以去搜一下他后来的辉煌战绩。那么 ResNet 为什么会有如此优异的表现呢?其实 ResNet 是解决了深度 CNN 模型难训练的问题,从图2中可以看到14年的VGG才19层,而 15 年的 ResNet 多达 152 层,这在网络深度完全不是一个量级上,所以如果是第一眼看这个图的话,肯定会觉得 ResNet 是靠深度取胜。事实当然是这样,但是 ResNet 还有架构上的 trick,这才使得网络的深度发挥出作用,这个 trick 就是残差学习(Residual learning)。下面详细讲述 ResNet 的理论及实现。
- 深度网络的退化问题
从经验来看,网络的深度对模型的性能至关重要,当增加网络层数后,网络可以进行更加复杂的特征模式的提取,所以当模型更深时理论上可以取得更好的结果,从图2中也可以看出网络越深而效果越好的一个实践证据。但是更深的网络其性能一定会更好吗?实验发现深度网络出现了退化问题(Degradation problem):网络深度增加时,网络准确度出现饱和,甚至出现下降。这个现象可以在图3中直观看出来:56层的网络比20层网络效果还要差。这不会是过拟合问题,因为56层网络的训练误差同样高。我们知道深层网络存在着梯度消失或者爆炸的问题,这使得深度学习模型很难训练。但是现在已经存在一些技术手段如BatchNorm来缓解这个问题。因此,出现深度网络的退化问题是非常令人诧异的。
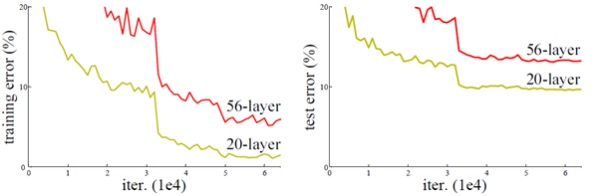
图3 - 20层与56层网络在CIFAR-10上的误差
- 残差学习
深度网络的退化问题至少说明深度网络不容易训练。但是我们考虑这样一个事实:现在你有一个浅层网络,你想通过向上堆积新层来建立深层网络,一个极端情况是这些增加的层什么也不学习,仅仅复制浅层网络的特征,即这样新层是恒等映射(Identity mapping)。在这种情况下,深层网络应该至少和浅层网络性能一样,也不应该出现退化现象。好吧,你不得不承认肯定是目前的训练方法有问题,才使得深层网络很难去找到一个好的参数。
这个有趣的假设让何博士灵感爆发,他提出了残差学习来解决退化问题。对于一个堆积层结构(几层堆积而成)当输入为 时其学习到的特征记为
,现在我们希望其可以学习到残差
,这样其实原始的学习特征是
。之所以这样是因为残差学习相比原始特征直接学习更容易。当残差为0时,此时堆积层仅仅做了恒等映射,至少网络性能不会下降,实际上残差不会为0,这也会使得堆积层在输入特征基础上学习到新的特征,从而拥有更好的性能。残差学习的结构如图4所示。这有点类似与电路中的“短路”,所以是一种短路连接(shortcut connection)。

图4 - 残差学习单元
为什么残差学习相对更容易,从直观上看残差学习需要学习的内容少,因为残差一般会比较小,学习难度小点。不过我们可以从数学的角度来分析这个问题,首先残差单元可以表示为:
其中 和
分别表示的是第
个残差单元的输入和输出,注意每个残差单元一般包含多层结构。
是残差函数,表示学习到的残差,而
表示恒等映射,
是ReLU激活函数。基于上式,我们求得从浅层
到深层
的学习特征为:
利用链式规则,可以求得反向过程的梯度:
式子的第一个因子 表示的损失函数到达
的梯度,小括号中的1表明短路机制可以无损地传播梯度,而另外一项残差梯度则需要经过带有weights的层,梯度不是直接传递过来的。残差梯度不会那么巧全为-1,而且就算其比较小,有1的存在也不会导致梯度消失。所以残差学习会更容易。要注意上面的推导并不是严格的证明。
- 直观理解为什么残差学习单元可以防止梯度消失。
首先,来看一下为什么会消失。我们知道,神经网络的训练无非就是前向传播和后向传播的过程,既然是传播,传递的过程中,总是会有损耗的,损耗过大,那么后面就接收不到什么东西了,也就更谈不上能学到东西,深度,也就没有了意义。
如上图,左边来了一辆装满了“梯度”商品的货车,来领商品的客人一般都要排队一个个拿才可以,如果排队的人太多,后面的人就没有了。于是这时候派了一个人走了“快捷通道”,到货车上领了一部分“梯度”,直接送给后面的人,这样后面排队的客人就能拿到更多的“梯度”。
- ResNet的网络结构
ResNet网络是参考了VGG19网络,在其基础上进行了修改,并通过短路机制加入了残差单元,如图5所示。变化主要体现在ResNet直接使用stride=2的卷积做下采样,并且用global average pool层替换了全连接层。ResNet的一个重要设计原则是:当feature map大小降低一半时,feature map的数量增加一倍,这保持了网络层的复杂度。从图5中可以看到,ResNet相比普通网络每两层间增加了短路机制,这就形成了残差学习,其中虚线表示feature map数量发生了改变。图5展示的34-layer的ResNet,还可以构建更深的网络如表1所示。从表中可以看到,对于18-layer和34-layer的ResNet,其进行的两层间的残差学习,当网络更深时,其进行的是三层间的残差学习,三层卷积核分别是1x1,3x3和1x1,一个值得注意的是隐含层的feature map数量是比较小的,并且是输出feature map数量的1/4。
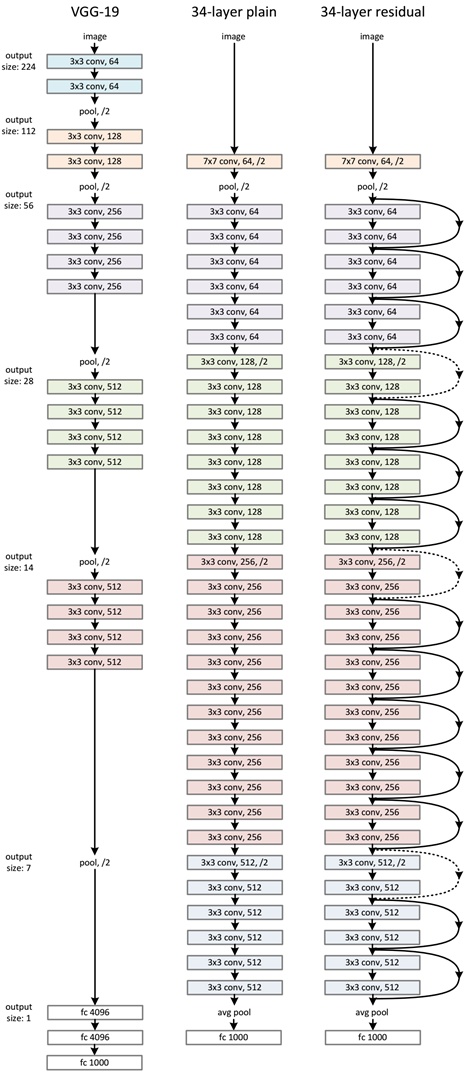
图5 - ResNet网络结构图
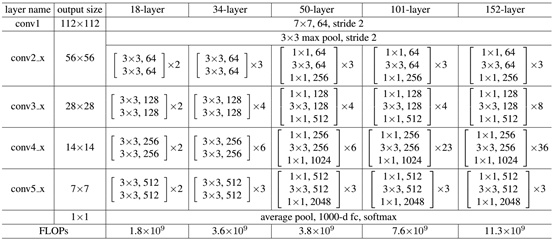
表1 - 不同深度的ResNet
下面我们再分析一下残差单元,ResNet使用两种残差单元,如图6所示。左图对应的是浅层网络,而右图对应的是深层网络。对于短路连接,当输入和输出维度一致时,可以直接将输入加到输出上。但是当维度不一致时(对应的是维度增加一倍),这就不能直接相加。有两种策略:
- 1. 采用zero-padding增加维度,此时一般要先做一个downsamp,可以采用strde=2的pooling,这样不会增加参数;
- 2. 采用新的映射(projection shortcut),一般采用1x1的卷积,这样会增加参数,也会增加计算量。短路连接除了直接使用恒等映射,当然都可以采用projection shortcut。
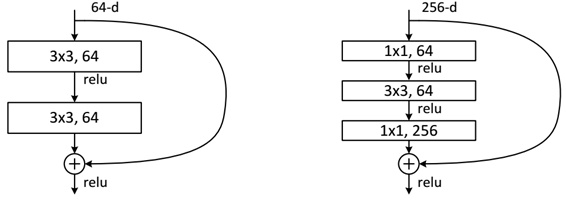
图6 - 不同的残差单元
作者对比18-layer和34-layer的网络效果,如图7所示。可以看到普通的网络出现退化现象,但是ResNet很好的解决了退化问题。

图7 - 18-layer和34-layer的网络效果
最后展示一下ResNet网络与其他网络在ImageNet上的对比结果,如表2所示。可以看到ResNet-152其误差降到了4.49%,当采用集成模型后,误差可以降到3.57%。
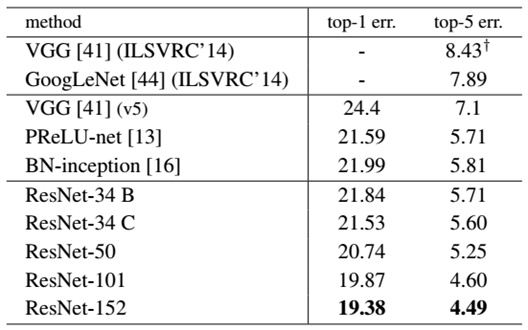
表2 - ResNet与其他网络的对比结果
说一点关于残差单元题外话,上面我们说到了短路连接的几种处理方式,其实作者在文献中又对不同的残差单元做了细致的分析与实验,这里我们直接抛出最优的残差结构,如图8所示。改进前后一个明显的变化是采用pre-activation,BN和ReLU都提前了。而且作者推荐短路连接采用恒等变换,这样保证短路连接不会有阻碍。感兴趣的可以去读读这篇文章。
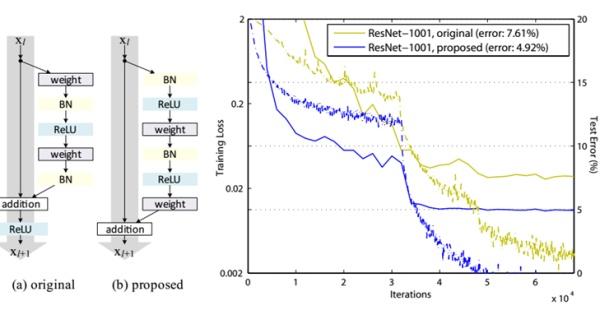
图8 - 改进后的残差单元及效果
Implement ResNet In TensorFlow
这里给出ResNet50的TensorFlow实现,模型的实现参考了Caffe版本的实现,核心代码如下:
class ResNet50(object):
def __init__(self, inputs, num_classes=1000, is_training=True,
scope="resnet50"):
self.inputs =inputs
self.is_training = is_training
self.num_classes = num_classes
with tf.variable_scope(scope):
# construct the model
net = conv2d(inputs, 64, 7, 2, scope="conv1") # -> [batch, 112, 112, 64]
net = tf.nn.relu(batch_norm(net, is_training=self.is_training, scope="bn1"))
net = max_pool(net, 3, 2, scope="maxpool1") # -> [batch, 56, 56, 64]
net = self._block(net, 256, 3, init_stride=1, is_training=self.is_training,
scope="block2") # -> [batch, 56, 56, 256]
net = self._block(net, 512, 4, is_training=self.is_training, scope="block3")
# -> [batch, 28, 28, 512]
net = self._block(net, 1024, 6, is_training=self.is_training, scope="block4")
# -> [batch, 14, 14, 1024]
net = self._block(net, 2048, 3, is_training=self.is_training, scope="block5")
# -> [batch, 7, 7, 2048]
net = avg_pool(net, 7, scope="avgpool5") # -> [batch, 1, 1, 2048]
net = tf.squeeze(net, [1, 2], name="SpatialSqueeze") # -> [batch, 2048]
self.logits = fc(net, self.num_classes, "fc6") # -> [batch, num_classes]
self.predictions = tf.nn.softmax(self.logits)
def _block(self, x, n_out, n, init_stride=2, is_training=True, scope="block"):
with tf.variable_scope(scope):
h_out = n_out // 4
out = self._bottleneck(x, h_out, n_out, stride=init_stride,
is_training=is_training, scope="bottlencek1")
for i in range(1, n):
out = self._bottleneck(out, h_out, n_out, is_training=is_training,
scope=("bottlencek%s" % (i + 1)))
return out
def _bottleneck(self, x, h_out, n_out, stride=None, is_training=True, scope="bottleneck"):
""" A residual bottleneck unit"""
n_in = x.get_shape()[-1]
if stride is None:
stride = 1 if n_in == n_out else 2
with tf.variable_scope(scope):
h = conv2d(x, h_out, 1, stride=stride, scope="conv_1")
h = batch_norm(h, is_training=is_training, scope="bn_1")
h = tf.nn.relu(h)
h = conv2d(h, h_out, 3, stride=1, scope="conv_2")
h = batch_norm(h, is_training=is_training, scope="bn_2")
h = tf.nn.relu(h)
h = conv2d(h, n_out, 1, stride=1, scope="conv_3")
h = batch_norm(h, is_training=is_training, scope="bn_3")
if n_in != n_out:
shortcut = conv2d(x, n_out, 1, stride=stride, scope="conv_4")
shortcut = batch_norm(shortcut, is_training=is_training, scope="bn_4")
else:
shortcut = x
return tf.nn.relu(shortcut + h)完整实现可以参见GitHub。