生活经验告诉我们,想要知道一个物体的长宽高,我们可以通过尺子测量。想要比较两个物体的质量,我们可以用天平来衡量。一切的一切,因为有了度量,而变得精准并且可比较。但现在我问你,如果在你的面前的是一本50万字的书,你能告诉我这本书包含了多少信息么?
这个时候,我们好像就陷入了沉思中,我们知道文字是信息的载体,而信息是看不见摸不着的东西,怎样可以给信息的多少定义呢?
Entropy
1948 年的香农祖师爷(Claude Shannon),和现在的我们一样,也在绞尽脑汁的想着如何解决这个难题。但是祖师爷毕竟是祖师爷,和我等凡人不同,他在著名的论文 “通讯的数学原理” 中,他提出了一个著名的概念,那就是信息熵(Entropy),即是基于一个随机事件出现的概率,来衡量信息的大小。一个随机事件的不确定度越高,它的信息熵也就越高。就是这个简单的“香农公式”的基本原理。让信息第一次有了大小了。而正是这个信息熵的概念,对后世的研究起到了无比重要的作用。

那么,那个流芳百世的香农公式,到底是什么呢?其实它的形式非常的简单,只是将概率和概率的对数相乘,然后求和取相反数即是了。
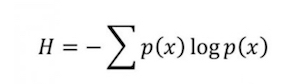
现在我们回归最开始的问题,一本50万字的中文书,究竟包含了多少信息呢?我们知道常用的汉字大概是有7000个。假如每个汉字出现的概率相等,那么我们大概需要13个字节来表示一个汉字(即是二进制的13位),那么每个汉字我们需要13比特来表示。但是实际上汉字的使用是不平衡的,前百分之十的汉字占用了百分之九十五的篇幅。所以根据香农的公式,实际上信息的含量大概会被降低到8到9个比特。如果我们再考虑一下上下文的关系,那么汉字的信息熵会变为大概5个比特。
50万字的书籍,所包含的信息就是250万比特,如果我们用一个比较好的压缩算法,整本书可以存成一个320K的文件。
可是光知道一本书的信息量有多少并没什么意义,和自然语言处理有什么关系呢?
好吧,我承认我有点跑题了,现在我就来介绍一下信息熵在自然语言中的运用。其实我现在回想起来,觉得信息熵的出现更多的是为了提供了 NLP 的理论基础。其实很多自然语言处理的方法是非常 intuitive 的,我们很容易会想到要这么去做,但是问为什么要这么做呢?往往就不太好解释了,而香农的这一套公式,则可以很好的解释他们。
Conditional Entropy
闲话不多说,首先来举个栗子。想象一个情景,你现在问小明一个问题,说你的脑袋里面正在构思着一个句子,让小明来猜这个句子里面都有些什么词组成。
小明会说,我擦嘞,中文词语成千上万,那么多的词,我怎么猜呀。这时候,你告诉他,这个句子里面有单词“我”。OK,小明开始思考,既然这个句子里面有了人称代词“我”,那么应该会出现个动词做谓语,于是小明开始猜这个句子里可能会有的谓语词,是“做”?是“去”?还是“爱”呢?等等等等。这时候,你又提供了他了这个句子里的另外一个词的信息,是“北京”,那么这个时候的小明就将一些不合理的动词选项排除掉了,比如“做”,因为“我做北京”,这个句子不合理。然后你又告诉小明,这个句子里还有一个词是“天安门”。“我?北京天安门”,哦,这个时候小明大概可以猜出来了,这个句子应该是“我爱北京天安门”。
从上面的故事,我们可以发现,好像一个单词,它是否会出现在句子中,是由它周围的词来决定的。比如前面和后面,出现了“我”和“北京天安门”,那么这个可能出现的词,好像就已经被限定死了,而不是任意词填进去都可以了。是不是很像我们小时候做的语文题,将一个句子中的一个部分挖去,然后我们来填空。

当一个句子的已知词越少,我们预测这个句子里的其他的难度越大,而知道的词越多,预测其他的词也就越容易。这也就是我们说的自由度下降了。利用信息熵的说法,当我们对一个句子一无所知的时候,它的熵值越大,而当我们知道的词越多,剩下的词的自由度越小,信息熵也在随之在下降。
这是不是已经很像我们的统计语言学模型了呢?
从信息熵的角度,我们来重新审视一下 word2vec,是不是觉得合理多了呢?
好,我们现在来利用公式来表示一下这个问题。这个时候,我们需要引入一个概念,叫做条件熵 ( conditional entropy )。
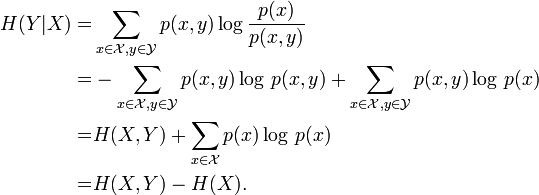
上图中的 X 和 Y 分别是一个句子中不同的两个词语,条件熵就是如果我们已知 X 存在这个句子中,Y 也出现在这个句子中的概率是多少。当然,这里所说的句子的概念,是广义的,你也可以是自定义一个 window size来说这是一个句子。

我们也可以证明,H(Y|X) <= H(Y),即是说,知道另外一个词 X 之后,词 Y 是否出现,这个事件的信息熵会下降。但我们看到还有等号的存在,聪明的你应该这时候会发现,当且仅当 X 和 Y 是完全独立的两个事件时,等号才成立。这也和我们的生活中的常识相对应。
以上我们都是讨论 X 和 Y 是两个词是否存在于一个句子中的情况。现在我们稍微扩展一下。
扩展一:主题模型 ( Topic Modeling )
主题模型是用于解决文档的分类问题的。如果现在我们已知的事件 X 不再是一个单词是否存在,而是这个句子是否是属于某一个类别,比如是体育类,是时事新闻类,等等。那么这样,单词 Y 出现在句子里的概率分布就会发生变化了。它的出现或者出现的概率就不是50%了。它的信息熵也会相对应的下降了。
主题模型中最经典的 Naive Bayes 算法,是根据单词出现在当前 Topic 的频率作为概率来推算,这也是根据最大期望模型 EM 算法来得出的结论。仔细想想,是不是也有条件熵模型的因素在里面呢?
扩展二:最大熵模型 ( MaxEnt )
我们已经知道,现实世界给与我们的信息越多,要预测的事件的信息熵值就会下降,相应的这个事件的发生概率也越来越趋于稳定,因为自由度下降了。最大熵模型就是这个原理。
在自然语言处理的命名实体识别问题当中,如果我给定的信息是,当前英文单词的前面一个词是at,并且是介词,当前单词的词性是名词且首字母是大写的,后面一个单词是句子的结束符。那么知道了这些信息的你,多半已经猜出这个当前单词的实体类别应该是地点 Location 了。
我们将一个一个的事件作为特征函数提取出来,然后根据事件发生的情况来发掘要预测事件的概率。特征越多,理论上预测也会越准。现在看上去,这是不是已经很像 CRF 算法的雏形了呀?
Mutual Information
“互信息”是信息熵的引申概念,它是对两个随机事件相关性的度量。比如说今天随机事件北京下雨和随机变量空气湿度的相关性就很大,但是和姚明所在的休斯敦火箭队是否能赢公牛队几乎无关。互信息就是用来量化度量这种相关性的。

这么看公式有些难以理解,我们换个形式。
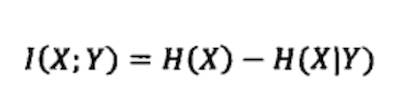
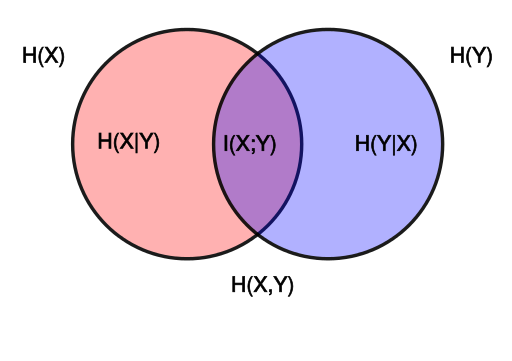
这个时候,看上去就简单多了,所谓的互信息,就是了解 Y 的情况下,对 X 的信息的消减情况的一个度量。
在自然语言处理中,经常要度量一些语言现象的相关性。比如在机器翻译中,最难的问题是词义的二义性(歧义性)问题。比如 Bush 一词可以是美国总统的名字,也可以是灌木丛。(有一个笑话,美国上届总统候选人凯里 Kerry 的名字被一些机器翻译系统翻译成了"爱尔兰的小母牛",Kerry 在英语中另外一个意思。)那么如何正确地翻译这个词呢?人们很容易想到要用语法、要分析语句等等。其实,至今为止,没有一种语法能很好解决这个问题。
真正实用的方法是使用互信息。具体的解决办法大致如下:首先从大量文本中找出和总统布什一起出现的互信息最大的一些词,比如总统、美国、国会、华盛顿等等,当然,再用同样的方法找出和灌木丛一起出现的互信息最大的词,比如土壤、植物、野生等等。有了这两组词,在翻译 Bush 时,看看上下文中哪类相关的词多就可以了。
Conclusion & Acknowledgement
这篇文章是我在上 Coursera 上伊利诺伊大学厄巴纳-香槟分校的 Text Mining and Analytics 这门课的时候,写下的一点感悟,文章中的部分内容有参考吴军的《数学之美》这本书的部分章节。再次对其表示感谢。
信息熵的概念,我在很久之前就已经接触过了,当时上本科的时候,并没有觉得它有什么用处。直到现在在自然语言处理的研究和工作中,发现它的用处几乎无处不再。再次给香农祖师爷献上我的膝盖。